POJ 2653 Pick-up sticks [线段相交 迷之暴力]

Pick-up sticks

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 12861		Accepted: 4847

Description

Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected. 

Input

Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed. 

Output

For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.

The picture to the right below illustrates the first case from input.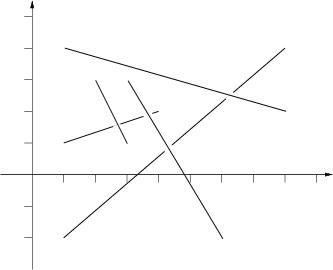 

Sample Input

5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
3
0 0 1 1
1 0 2 1
2 0 3 1
0

Sample Output

Top sticks: 2, 4, 5.
Top sticks: 1, 2, 3.

Hint

Huge input,scanf is recommended.

Source

Waterloo local 2005.09.17

---

还是判断线段相交

注意两条线段共线的情况，用点积判断

太诡异从后往前暴力判断能过，用一个栈维护当前没有覆盖的线段也能过

但是最坏复杂度都是N^2啊？？？

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
const int N=1e5+;
const double eps=1e-;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}
inline int sgn(double x){
    if(abs(x)<eps) return ;
    else return x<?-:;
}
struct Vector{
    double x,y;
    Vector(double a=,double b=):x(a),y(b){}
    bool operator <(const Vector &a)const{
        return x<a.x||(x==a.x&&y<a.y);
    }
    void print(){
        printf("%lf %lf\n",x,y);
    }
};
typedef Vector Point;
Vector operator +(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator -(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator *(Vector a,double b){return Vector(a.x*b,a.y*b);}
Vector operator /(Vector a,double b){return Vector(a.x/b,a.y/b);}
bool operator ==(Vector a,Vector b){return sgn(a.x-b.x)==&&sgn(a.y-b.y)==;}

double Cross(Vector a,Vector b){
    return a.x*b.y-a.y*b.x;
}
double Dot(Vector a,Vector b){
    return a.x*b.x+a.y*b.y;
}
double DisPP(Point a,Point b){
    Point t=a-b;
    return sqrt(t.x*t.x+t.y*t.y);
}
struct Line{
    Point s,t;
    Line(){}
    Line(Point p,Point v):s(p),t(v){}
}l[N];
bool isLSI(Line l1,Line l2){
    Vector v=l1.t-l1.s,u=l2.s-l1.s,w=l2.t-l1.s;
    return sgn(Cross(v,u))!=sgn(Cross(v,w));
}
bool isSSI(Line l1,Line l2){
    Vector v1=l1.t-l1.s,v2=l2.t-l2.s;
    if(sgn(Cross(v1,v2))==){
        int flag=;
        Vector u=l2.s-l1.s,w=l2.t-l1.s;
        if(sgn(Dot(u,w))<) flag=;
        u=l2.s-l1.t,w=l2.t-l1.t;
        if(sgn(Dot(u,w))<) flag=;
        return flag;
    }
    else return isLSI(l1,l2)&&isLSI(l2,l1);
}

int n;
bool vis[N];
double x,y,x2,y2;
int main(int argc, const char * argv[]) {
    while(true){
        memset(vis,,sizeof(vis));
        n=read(); if(n==) break;
        for(int i=;i<=n;i++){
            scanf("%lf%lf%lf%lf",&x,&y,&x2,&y2);
            l[i]=Line(Point(x,y),Point(x2,y2));
        }
        for(int i=;i<=n;i++){
            for(int j=i+;j<=n;j++) if(isSSI(l[j],l[i])){vis[i]=;break;}
        }
        printf("Top sticks: ");
        int fir=;
        for(int i=;i<=n;i++) if(!vis[i]){
            if(fir) printf("%d",i),fir=;
            else printf(", %d",i);
        }
        puts(".");
    }
    return ;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
const int N=1e5+;
const double eps=1e-;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}
inline int sgn(double x){
    if(abs(x)<eps) return ;
    else return x<?-:;
}
struct Vector{
    double x,y;
    Vector(double a=,double b=):x(a),y(b){}
    bool operator <(const Vector &a)const{
        return x<a.x||(x==a.x&&y<a.y);
    }
    void print(){
        printf("%lf %lf\n",x,y);
    }
};
typedef Vector Point;
Vector operator +(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator -(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator *(Vector a,double b){return Vector(a.x*b,a.y*b);}
Vector operator /(Vector a,double b){return Vector(a.x/b,a.y/b);}
bool operator ==(Vector a,Vector b){return sgn(a.x-b.x)==&&sgn(a.y-b.y)==;}

double Cross(Vector a,Vector b){
    return a.x*b.y-a.y*b.x;
}
double Dot(Vector a,Vector b){
    return a.x*b.x+a.y*b.y;
}
double DisPP(Point a,Point b){
    Point t=a-b;
    return sqrt(t.x*t.x+t.y*t.y);
}
struct Line{
    Point s,t;
    Line(){}
    Line(Point p,Point v):s(p),t(v){}
}l[N];
bool isLSI(Line l1,Line l2){
    Vector v=l1.t-l1.s,u=l2.s-l1.s,w=l2.t-l1.s;
    return sgn(Cross(v,u))!=sgn(Cross(v,w));
}
bool isSSI(Line l1,Line l2){
    Vector v1=l1.t-l1.s,v2=l2.t-l2.s;
    if(sgn(Cross(v1,v2))==){
        int flag=;
        Vector u=l2.s-l1.s,w=l2.t-l1.s;
        if(sgn(Dot(u,w))<) flag=;
        u=l2.s-l1.t,w=l2.t-l1.t;
        if(sgn(Dot(u,w))<) flag=;
        return flag;
    }
    else return isLSI(l1,l2)&&isLSI(l2,l1);
}

int n,st[N],top;
inline void del(int p){
    for(int i=p;i<=top;i++) st[i]=st[i+];top--;
}
double x,y,x2,y2;
int main(int argc, const char * argv[]) {
    while(true){
        top=;
        n=read(); if(n==) break;
        for(int i=;i<=n;i++){
            scanf("%lf%lf%lf%lf",&x,&y,&x2,&y2);
            l[i]=Line(Point(x,y),Point(x2,y2));
            for(int j=;j<=top;j++) if(isSSI(l[st[j]],l[i])) del(j),j--;
            st[++top]=i;
        }
        printf("Top sticks: %d",st[]);
        for(int i=;i<=top;i++) printf(", %d",st[i]);
        puts(".");
    }
    return ;
}