2018.07.03 POJ 1279Art Gallery（半平面交）

Art Gallery

Time Limit: 1000MS Memory Limit: 10000K

Description

The art galleries of the new and very futuristic building of the Center for Balkan Cooperation have the form of polygons (not necessarily convex). When a big exhibition is organized, watching over all of the pictures is a big security concern. Your task is that for a given gallery to write a program which finds the surface of the area of the floor, from which each point on the walls of the gallery is visible. On the figure 1. a map of a gallery is given in some co-ordinate system. The area wanted is shaded on the figure 2.



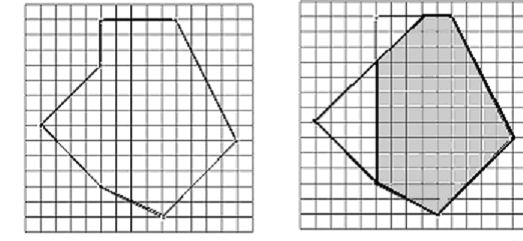
Input

The number of tasks T that your program have to solve will be on the first row of the input file. Input data for each task start with an integer N, 5 <= N <= 1500. Each of the next N rows of the input will contain the co-ordinates of a vertex of the polygon ? two integers that fit in 16-bit integer type, separated by a single space. Following the row with the co-ordinates of the last vertex for the task comes the line with the number of vertices for the next test and so on.

Output

For each test you must write on one line the required surface - a number with exactly two digits after the decimal point (the number should be rounded to the second digit after the decimal point).

Sample Input

1

7

0 0

4 4

4 7

9 7

13 -1

8 -6

4 -4

Sample Output

80.00

Source

Southeastern Europe 2002

这又是一道基础的计算几何题，准确的说，这就是求半平面交的裸板，这也是本蒟蒻第一次写半平面交这个东西。这里简单提一下半平面交的求法吧。

首先，我们将所有半平面按照极角排序，然后用类似极角排序求凸包的方法来求半平面交，但区别是求凸包只需要使用一个栈，而现在我们需要维护的是一个双端队列。为什么呢？因为如果我们当前再放入一个半平面，它会对队首和队尾的半平面都产生影响（没懂的可以画个图感受一下）。什么时候我们会从队列中弹出半平面中呢？显然需要判断前两个半平面的交点和该半平面的关系，如果点在半平面右侧就弹出直到弹不动或者队列为空为止。然后实现时会有一些比较烦的细节，但总的来说写起来还是比较愉快的。

我们要注意这道题的一些坑点：首先点可能按顺时针或者逆时针给出，这样的话我们要先按一定顺序求一遍原多边形的面积来调整每个半平面的方向。其次，本蒟蒻在POJ上一直WA，对着其他大佬的代码改也过不了，最后无奈将printf函数中的lf改成了f就过了，这个真的是玄学错误了。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define eps 1.0e-12
#define N 1505
using namespace std;
int t,n,q[N];
struct point{double x,y;}p[N];
struct line{point a,b;double poa;}l[N];
inline point operator-(point a,point b){return point{a.x-b.x,a.y-b.y};}
inline double cross(point a,point b){return a.x*b.y-b.x*a.y;}
inline point across(line a,line b){
    double a1=cross(b.b-a.a,b.a-a.a),a2=cross(b.a-a.b,b.b-a.b);
    return point{(a2*a.a.x+a1*a.b.x)/(a2+a1),(a2*a.a.y+a1*a.b.y)/(a2+a1)};
}
inline bool check(point a,line b){return cross(a-b.a,b.b-b.a)>0;}
inline bool cmp(line a,line b){
    if(fabs(a.poa-b.poa)<eps)return cross(a.b-b.a,b.b-b.a)<0;
    return a.poa<b.poa;
}
inline double solve(){
    sort(l+1,l+n+1,cmp);
    int siz=0,head=1,tail=1;
    for(int i=1;i<=n;++i)
        if(fabs(l[i-1].poa-l[i].poa)>eps)l[++siz]=l[i];
    q[1]=1;
    for(int i=2;i<=siz;++i){
        while(head<tail&&check(across(l[q[tail-1]],l[q[tail]]),l[i]))--tail;
        while(head<tail&&check(across(l[q[head]],l[q[head+1]]),l[i]))++head;
        q[++tail]=i;
    }
    while(head<tail&&check(across(l[q[tail-1]],l[q[tail]]),l[q[head]]))--tail;
    while(head<tail&&check(across(l[q[head]],l[q[head+1]]),l[q[tail]]))++head;
    if(tail-head<=1)return 0.00;
    else{
        for(int i=head;i<tail;++i)p[i-head+1]=across(l[q[i]],l[q[i+1]]);
        p[tail-head+1]=across(l[q[tail]],l[q[head]]);
        double ans=0.0;
        for(int i=1;i<=tail-head;++i)ans+=cross(p[i],p[i+1]);
        ans+=cross(p[tail-head+1],p[1]);
        return ans/2.0;
    }
}
int main(){
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        for(int i=1;i<=n;++i)scanf("%lf%lf",&p[i].x,&p[i].y);
        double area=0.0;
        for(int i=1;i<n;++i){
            l[i].a=p[i],l[i].b=p[i+1];
            area+=cross(p[i],p[i+1]);
        }
        l[n].a=p[n],l[n].b=p[1];
        area+=cross(p[n],p[1]);
        if(area<0.0)for(int i=1;i<=n;++i)swap(l[i].a,l[i].b);
        for(int i=1;i<=n;++i)l[i].poa=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
        printf("%.2f\n",solve());
    }
    return 0;
}