排序算法(2) 堆排序 C++实现

堆

1 数组对象

2 可以视为一棵完全二叉树

3 一个堆可以被看作一棵二叉树和一个数组，如下图所示：

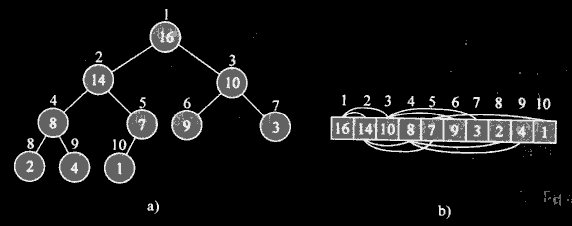
4 下标计算（通常使用内联函数或者宏来定义下标操作）：

• 已知某个结点的下标为i
• 其父节点下标：i/2向下取整
• 左孩子下标：2i
• 右孩子下标：2i+1

5 最大堆：除根节点以外的每个节点i，有A[PARENT(i)] >= A[i]

最小堆：除根节点意外的每个节点i，有A[PARENT(i)] <= A[i]

---

堆排序

步骤：

1. 建大顶堆
2. 去堆顶元素与当前堆的最后一个元素进行互换。
3. 该堆顶元素已达最终位置，排除出堆
4. 对剩下的堆进行最大堆调整
5. 重复2到4步

排序过程

1 建堆过程

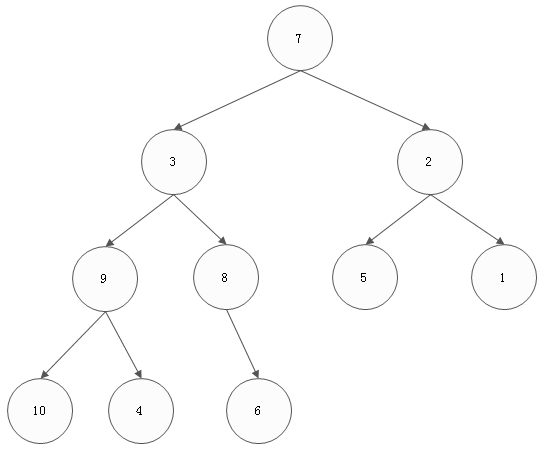
1） 从第一个非叶子节点开始，对value为8的节点进行调整，无需调整。

2） 对value值为9的节点进行调整。

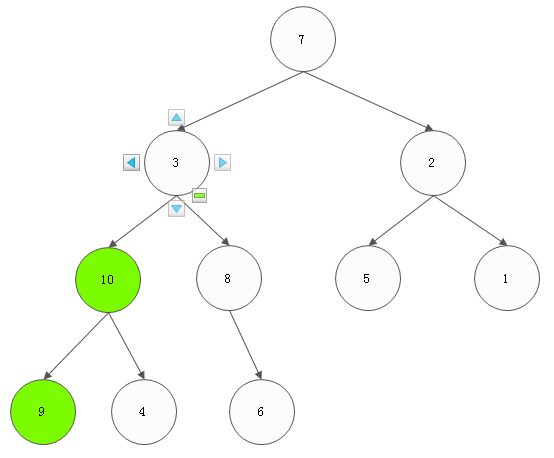
3） 对value为2的节点调整

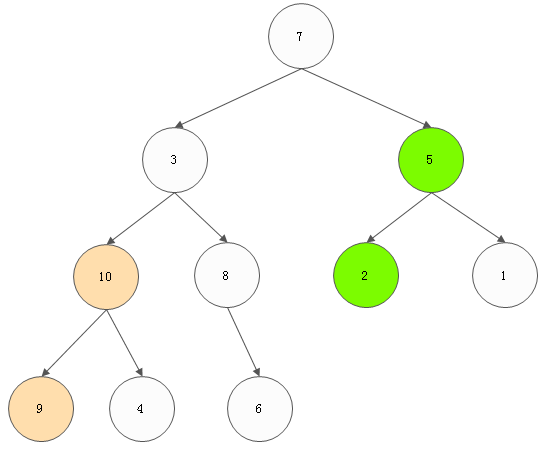
4） 对value为3的节点进行调整

     ----》

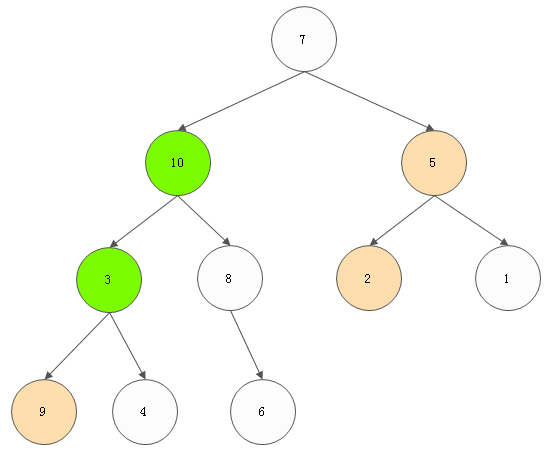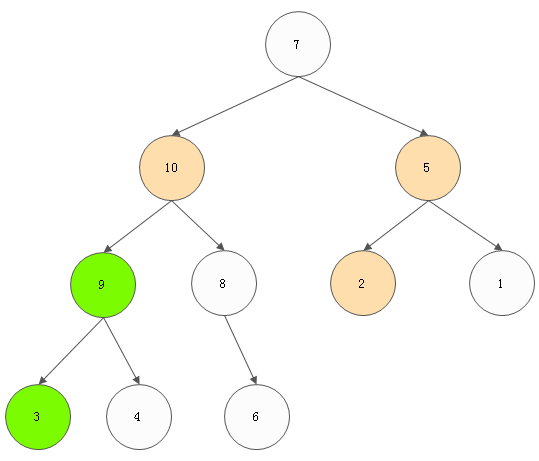
5） 对value为7的节点进行调整

  ---》

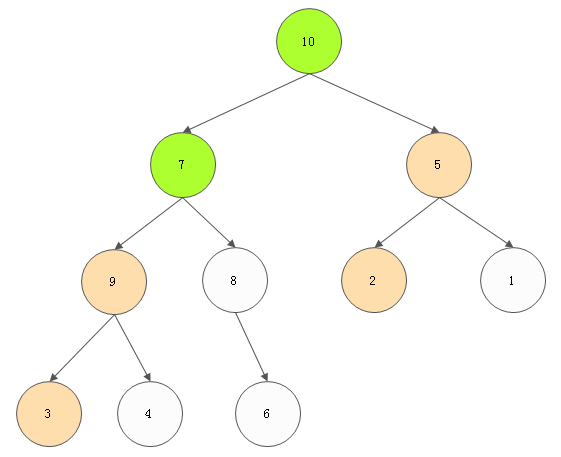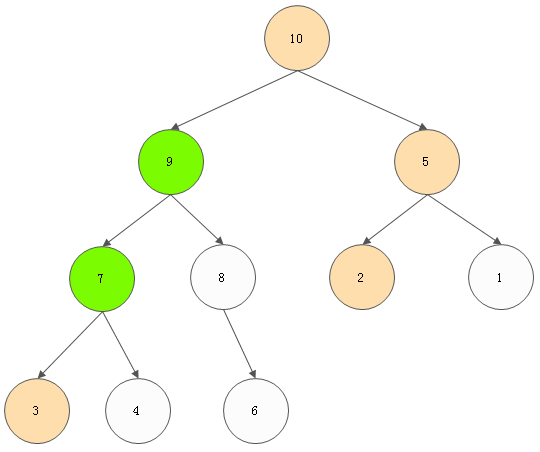
建堆完成

2 堆顶元素与当前堆的最后一个元素进行互换。

3 该堆顶元素已达最终位置，排除出堆

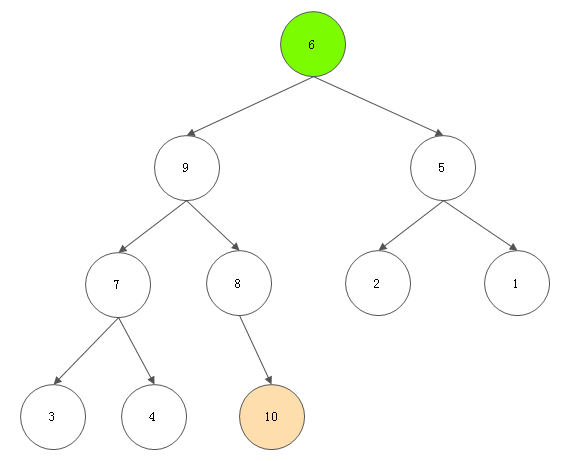
4 对剩下的堆进行调整

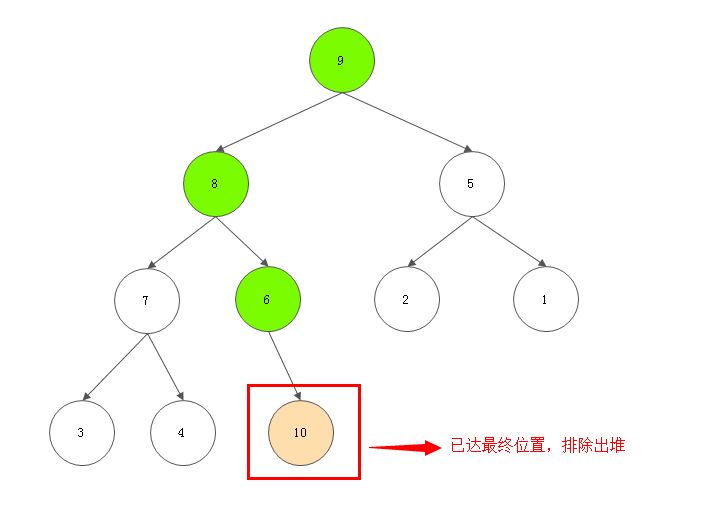
递归进行堆首和堆尾互换以及调整堆的步骤，结果即为排好序的堆。

---

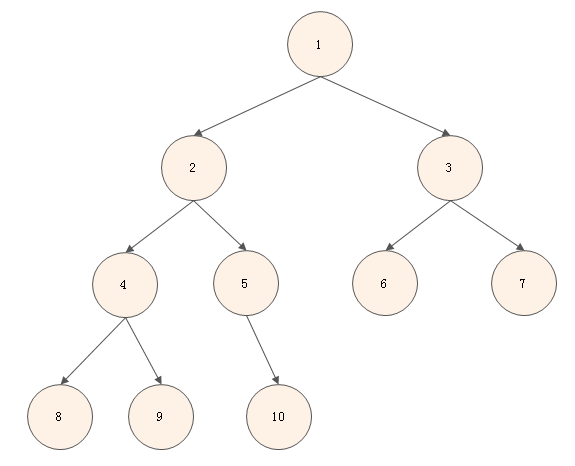
代码实现

// heapsort.h
class HeapSort:public BaseSort {
public:
    HeapSort(int Array[], int len) : BaseSort() {
        this->Array = Array;
        this->len = len;
    }
    void sort();
private:
    /* 建堆 */
    void buildMaxHeap();

    /* 调整堆，以保持最大堆性质 */
    void maxHeapIfy( int i , int curlen);

    /* 堆排序 */
    void heapSort();

    /* 返回父节点下标 */
    int Parent(int i) {
        if ( i % 2 == 0 )
            return i/2;
        else
            return i/2 + 1;
    };

    /* 返回左孩子节点下标 */
    int Left(int i) { return 2 * i + 1; };

    /* 返回右孩子节点下标 */
    int Right(int i) { return 2 * i + 2; };
private:
    int* Array;
    int len;
};

相关成员函数实现

// heapsort.cpp
#include "heapsort.h"
void HeapSort::sort() {
    heapSort();
}
void HeapSort::heapSort() {

    buildMaxHeap();
    int i = this->len;
    int tmp;
    while( i > 0 ) {
        tmp = this->Array[0];
        this->Array[0] = this->Array[i-1];
        this->Array[i-1] = tmp;
        i--;
        maxHeapIfy(0, i);
    }
}
void HeapSort::maxHeapIfy( int i, int curlen ) {
    int left, right, largest;
    int tmp;
    left = Left(i);
    right = Right(i);
    if ( left < curlen-1
        && Array[left] > Array[i])
        largest = left;
    else
        largest = i;
    if ( right < curlen-1
        && Array[right] > Array[largest])
        largest = right;
    if ( largest != i ) {
        tmp = Array[i];
        Array[i] = Array[largest];
        Array[largest] = tmp;
        maxHeapIfy(largest, curlen);
    }
}
void HeapSort::buildMaxHeap() {
    int i;
    for ( i = (len-1)/2 ; i >= 0; i-- ) {
        maxHeapIfy(i, len);
        if (DEBUG) {
            printArray(this->Array, this->len, "midResult");
        }
    }
}

测试代码：

 /* --------- HeapSort -------- */
int b[10] = {7,3,2,9,8,5,1,10,4,6};
HeapSort* heapsort = new HeapSort(b, len);
heapsort->sort();
printArray(b, len, "HeapSort ");

---

参考资料：

《算法导论 2rd》

http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html  《算法导论》读书笔记之第6章 堆排序