Sunday算法[原创]

一.应用：

　　同样的，sunday算法也是在一个字符串中查找另一个字符串出现的首地址，是Daniel M.Sunday于1990年提出的，从销量上讲，Sunday>BM>KMP,是这类问题的最优解。在实用上，KMP算法并不比最简单的c库函数strstr()快多少，而BM算法则往往比KMP算法快上3－5倍。

二.核心思想：

　　在匹配过程中，模式串并不被要求一定要按从左向右进行比较还是从右向左进行比较，它在发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率(算法思想很简单)。与BM算法相仿，有点像其删减版，所以其时间复杂度和BM算法差不多，平均性能的　时间复杂度也为O(n)，最差情况的时间复杂度为O(n * m)，但是要容易理解的多。

　　Sunday的算法思想和Horspool有些相似，但是。当出现不匹配的时候，却不是去找匹配串中不匹配的字符在模式串的位置，而是直接找最右边对齐的右一位的那个字符在模式串的位置。

三.算法解析：

　　以下面的例子进行具体说明：

源串    ：a b  c d  f  h g  e d e w o f d e w o n d e k

匹配串：e w o n  d  e

^

显然，第一个字符不匹配，肯定要把子串往后移动。但是该移动多少呢？对于Sunday来讲，要看的是当前字串后面的那个绿色的 g,判断g是否在匹配串中出现，结论是没有，则说明可以直接跳过一大段，从g之后的字符开始进行比较，得到下图：

源串    ：a b  c d  f  h g e d e w o f d e w o n d e k

匹配串：                       e w o n d e

^

在匹配串中，字符’e’出现两次，按照原理，选择最右位置出现的’e’进行对齐，那么可以得到下图：

源串    ：a b  c d  f  h g e d e w o f d e w o n d e k

匹配串：       e w o n d e

^

第一个字符就不匹配，我们接下来要观察的则是d,d在匹配串中出现了，将d对齐

源串    ：a b  c d  f  h g e d e w o f d e w o n d e k

匹配串：              e w o nd e

^

结果第一个字符就不相等，那么我们要看的依然是当前字符串后面的第一个字符w,这次w在匹配串中出现了，则对齐最右边的w(本例中w只有一个)

源串    ：a b  c d  f  h g e d e w o f d e w o n d e k

匹配串：                             e w o n d e

^

在匹配到第四个字符时，f与n不相等，则要考察的是当前字串后面的那个绿色的w,将w对齐，则匹配成功。

源串    ：a b  c d  f  h g e d e w o f d e w o n d e k

匹配串：                                            e w o n d e

^

四.代码实现：

因为char是1 个字节，所以我们将数组开到256，char类型最大不能超过256位。

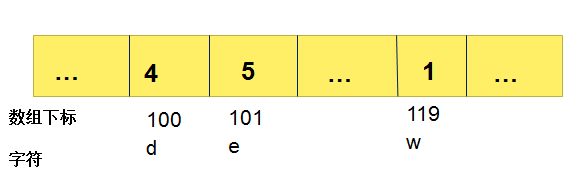
开辟一个有256个元素的数组，用于存放各种字符，下标对应相应字符，如a对应的下标为97，e对应的下标就为101（与ASCII码值对应），该数组里面放的是该字符在匹配串从右向左第一次出现的位置下标。如图：

 #include<stdio.h>
 #include<stdlib.h>
 #include<string.h>

 int *GetNext(char *str)
 {
     int *pNext = NULL;
     pNext = (int *)malloc(sizeof(int)*);
     memset(pNext,-,sizeof(int)*);

     //从右向左第一次出现的下标
     int i = ;
     for(i = ;i<strlen(str);i++)
     {
         pNext[str[i]] = i;//只需不断赋值就可以保证pnext数组中存入的是最右边的值
     }
     return pNext;
 }

 int Sunday(char *src,char *match)
 {
     if(src == NULL || match == NULL)return -;

     //获得next数组
     int *pNext = NULL;
     pNext = GetNext(match);

     int i; //遍历主串
     int j; //遍历匹配串的
     int k; //每一次进行匹配时，匹配串的头在源串中对应的位置（每一次匹配的开始位置，红色字母）

     i = ;
     j = ;

     while(i < strlen(src) && j < strlen(match))
     {
         k  = i;//随着匹配向后进行，不断更新每次匹配的开始位置
         while(src[i] == match[j])
         {
             i++;
             j++;
         }
         if(j == strlen(match))
         {
             return i-j;
         }
         else
         {　　//实现对齐
             //k+strlen(match):找到主串对应匹配串的下一位置（对应图解中的绿色字符）
             //pnext[src[k+strlen(match)]]找到当前字符在匹配串中第一次出现的下标，相减
             i = k+strlen(match) - pNext[src[k+strlen(match)]];//表面是相同字符对齐，实际上确定了新的起始位置
             j = 0;
         }
     }
     return -;
 }

 int main()
 {
     int n;
     n = Sunday("abcabcdabcabceabcabcdabcabcadshfoiewr","abcabcdabcabca");
     printf("%d\n",n);
     return ;
 }