图(树)的深度优先遍历dfs

图的深度优先遍历

深度优先，即对于一个图或者树来说，在遍历时优先考虑图或者树的单一路径的深度。示意图如下

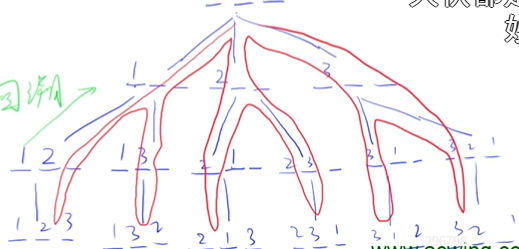
即深度优先搜索的核心就是对一个路径一直向下搜索，当搜索到头时就回溯到前一状态再寻找别的路

深搜问题一般有两种情况，一种是搜索时元素只能用有限次，这需要我们定义一个全局标记数组来对已经使用的数字进行标记。

如该题 排列数字

这道题的解法就是使用dfs枚举各种情况。当dfs时，其实就是在遍历一棵使用递归建成的搜索树。

题解代码如下

#include <iostream>
using namespace std;
const int N = 20;
int ans[N]; //答案存储数组
int n;
int cnt;    //答案个数记录，用于写递归出口
bool check[N]; // 标记
void dfs()
{
    if(cnt == 3)
    {
        for(int i = 0 ; i < 3 ; i++)
            cout << ans[i] << ' ';
        cout << '\n';
	return；
    }
    for(int i = 1 ; i <= n ; i++)
    {
        if(!check[i])
        {
            ans[cnt++] = i;
            check[i] = true;
            dfs();
            /*回溯*/
            check[i] = false;
            cnt --;
        }
    }
}
int main()
{
    cin >> n;
    dfs();
    return 0;
}

注意！当dfs时一定别忘了写递归出口，递归出口的条件一般就为题目要求的筛选条件

dfs函数中的for循环其实就是枚举每一层的各种情况。

其实本道题还有更为方便的解法，利用algorithm库中的next_permutation函数可以轻松的解决字典序全排列问题。

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int ans[N]; //答案存储数组
int n;
int main()
{
    cin >> n;
    for(int i = 0 ; i <= n ; i++ )
        ans[i] = i + 1;
    do
    {
        for(int i = 0 ; i < n ; i++)
            cout << ans[i] << ' ';
        cout << '\n';
    }while(next_permutation(ans, ans+n));
    return 0;
}

该函数的作用请见next_permutation