机器学习-线性分类-支持向量机SVM-软间隔-核函数-13
1. 总结 SVM
SVM算法的基础是感知器模型,
感知器模型 与 逻辑回归的不同之处?
逻辑回归 sigmoid(θx) 映射到 0-1之间给出预测概率
感知器分类 sign(θx) 输出θx的符号, +1 或者-1 给出x是属于正样本还是负样本
直接输出 θx的值就是 线性回归
感知器 模型 只要能将寻找到这样的一个超平面 将正样本与负样本能够区分开来就行,
而SVM不仅要能区分 而且还要能使得 距离超平面最进的点 到达这样的一个超平面距离最大

这也就是一个 二次优化的问题, 先找最近的点,再通过这些最近的点,确定最终的超平面。
显然 SVM 具有比 感知器 更优的泛化能力
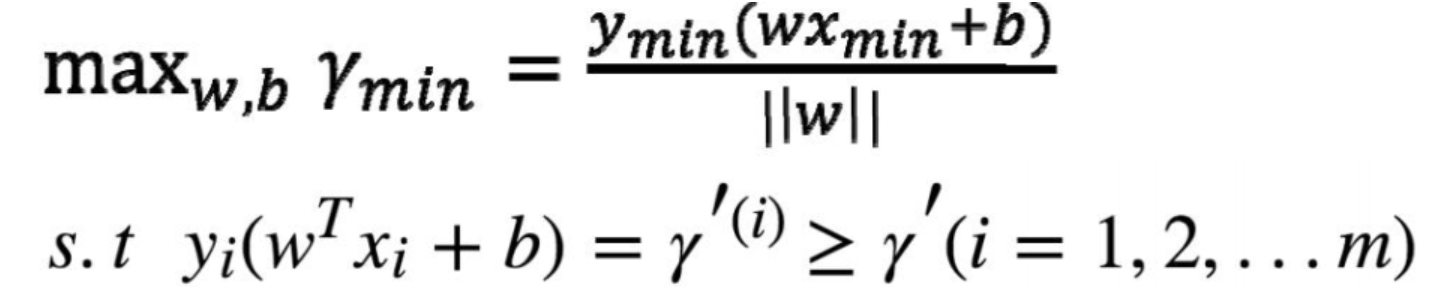
寻找这样的 模型参数 w b(也就是θ), 使得 最近的点 Xmin Ymin 到达 参数确定的的平面 距离尽可能的远,这样得到的参数θ 就是最终的完美的
仔细品味下这张图:

超平面的法向量 w 是方向的 通过W b 就能唯一确定一个平面
简单总结下:
求解W b 转化成 求解α*
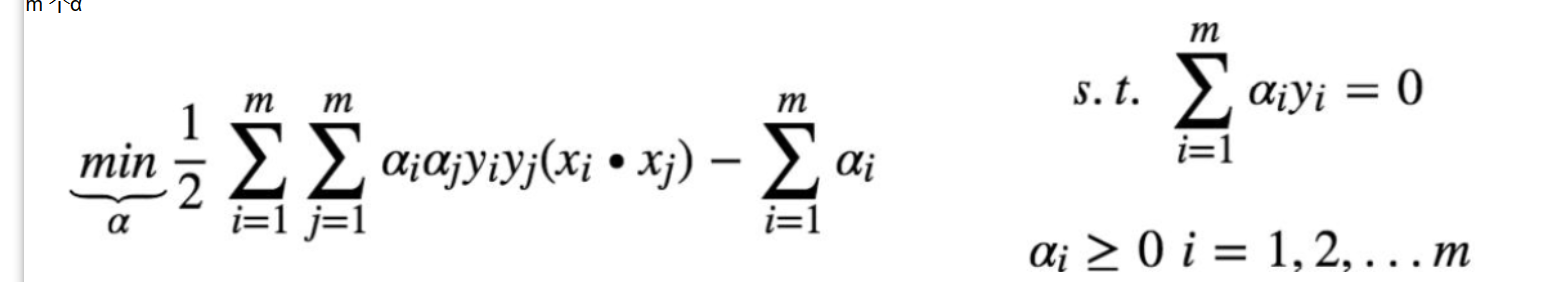
m条样本 就有m个α

α求得之后 可直接 求得W

通过那些不为0的α 带入后 可求得b 取平均 得到b
以上的求解 叫做 硬间隔SVM
下面讲解 软间隔svm
2. 软间隔svm
有些时候 噪声 会造成 线性 不可分
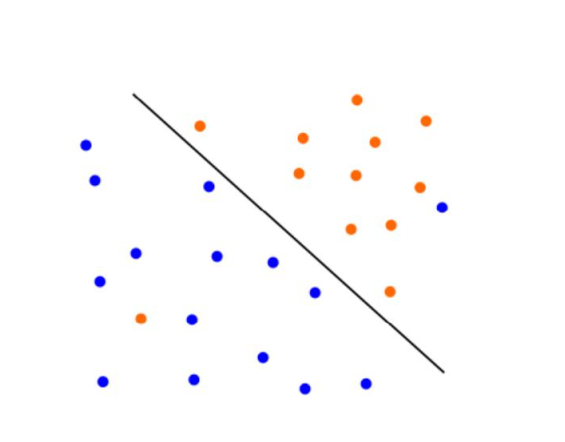
正样本 负样本 在边界处 相互渗透 这就导致 没法用 上面的SVM 意味着找不到一个合格的超平面
引入松弛变量 提出松弛变量ξi≥0(每个数据点自己有一个ξi)
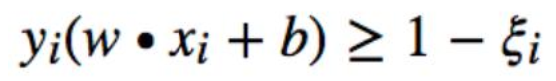
这样就至少肯定有好多的 w 和 b 满足条件了
ξ代表异常点嵌入间隔面的深度, 我们要在能选出符合约束条件的最好的 w 和 b 的同时,让
嵌入间隔面的总深度越少越好
问题转化成:
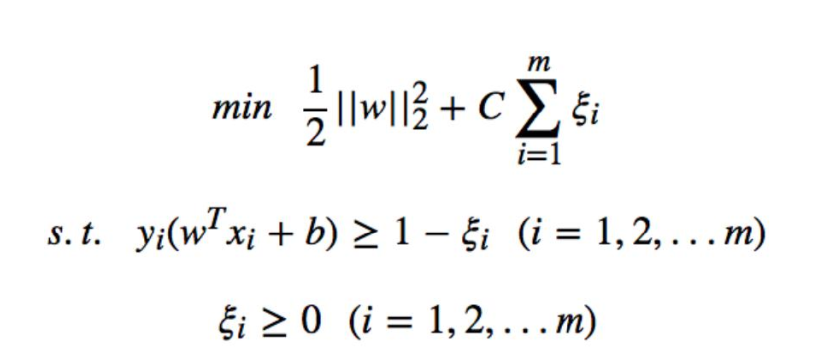
约束条件 变成了两个
构造拉格朗日函数:
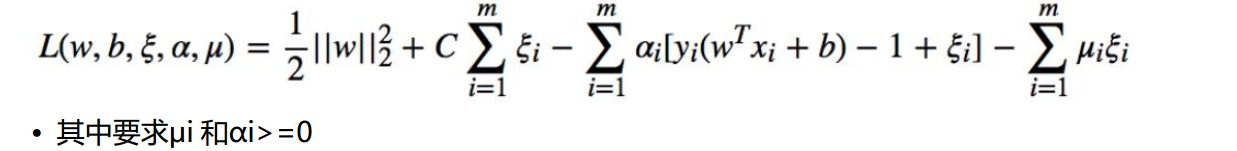

问题转化成对偶问题:
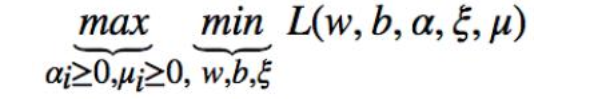
先求 L 函数对 w,b,ξ的极小值,再求其对α和μ的极大值
得到:

与硬间隔 SVM一样的表达式 只不过约束条件不一样
最终问题换成:

与之前相比,只是多了个约束条件而已,仍然可以使用 SMO 来求解
结论:

C是一个系数 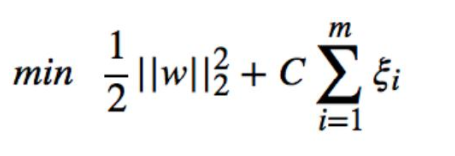
损失函数两部分更侧重于哪一部分
4. 核函数
线性 SVM 来说,判别函数为:
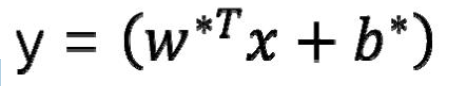
由于:
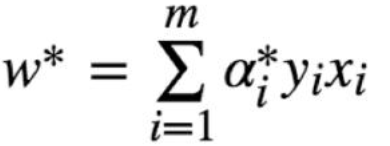
代入后得到:
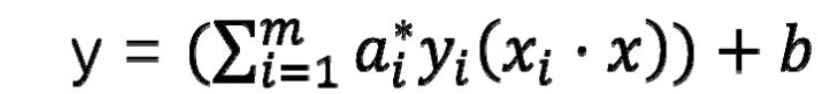
每一次在计算判别函数结果时需要求得待判断点和所有训练集样本点的內积 xi*x 这里铺垫一下对于升维 需要用到这个结果
升维是一种处理线性不可分问题的方式,我们通过把原始的 x 映射到更高维空间φ(x)上
比如多项式回归:可以将 2 元特征(x1,x2) 映射为 5 元特征(x1,x2,x1*x2,x12,x22) 这样在五元空间中有
些二元空间里线性不可分的问题就变得线性可分了
但是对于SVM如何做升维?
升维示意图:
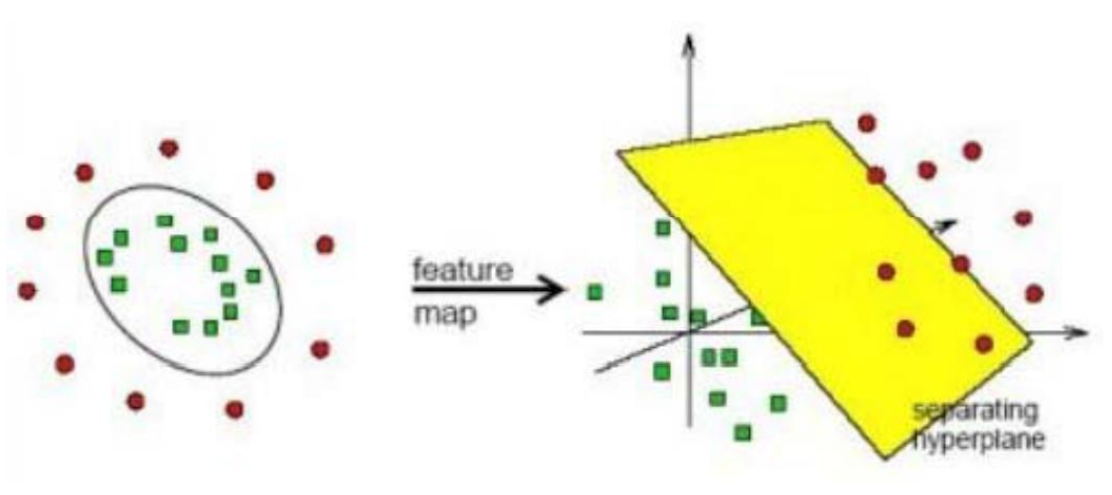
看似这种升维方式已经完美解决了线性不可分问题,但是带来了一个新问题
假设就使用多项式回归的方式进行升维:对于二维 x1,x2 升维后的结果是:
x1,x2,x1*x2,x12,x22
假如是三维数据 x1,x2,x3 呢?
19 维!升维之后还需要做向量的内积,时间空间消耗就更可怕了
低维度的计算 就能得到升维后的结果!!!
定义: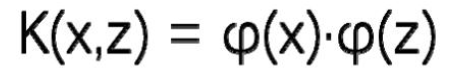
问题就转化成:
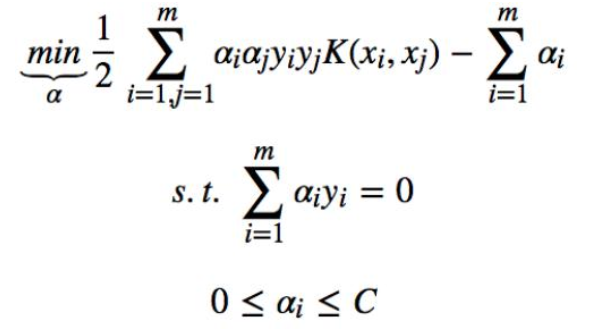
判别式转化成:
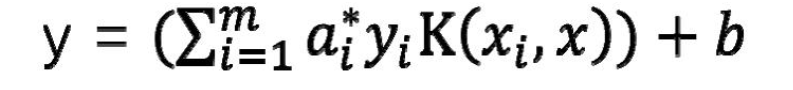
常用的核函数:
线性核函数: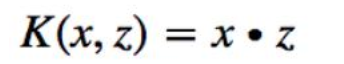
高斯核函数:
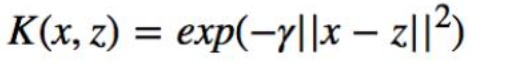
多项式核函数:
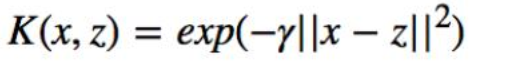
sigmoid核函数(-1, +1)之间的s型曲线 与逻辑回归的sigmoid(0,1)不同而已:
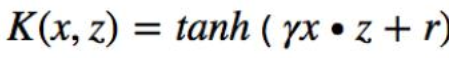
机器学习-线性分类-支持向量机SVM-软间隔-核函数-13的更多相关文章
- 线性可分支持向量机与软间隔最大化--SVM(2)
线性可分支持向量机与软间隔最大化--SVM 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 我们说可以通过间隔最 ...
- 机器学习,详解SVM软间隔与对偶问题
今天是机器学习专题的第34篇文章,我们继续来聊聊SVM模型. 我们在上一篇文章当中推导了SVM模型在硬间隔的原理以及公式,最后我们消去了所有的变量,只剩下了\(\alpha\).在硬间隔模型当中,样本 ...
- 统计学习:线性可分支持向量机(SVM)
模型 超平面 我们称下面形式的集合为超平面 \[\begin{aligned} \{ \bm{x} | \bm{a}^{T} \bm{x} - b = 0 \} \end{aligned} \tag{ ...
- 线性可分支持向量机--SVM(1)
线性可分支持向量机--SVM (1) 给定线性可分的数据集 假设输入空间(特征向量)为,输出空间为. 输入 表示实例的特征向量,对应于输入空间的点: 输出 表示示例的类别. 线性可分支持向量机的定义: ...
- 机器学习笔记:支持向量机(svm)
支持向量机(svm)英文为Support Vector Machines 第一次接触支持向量机是2017年在一个在线解密游戏"哈密顿行动"中的一个关卡的二分类问题,用到了台湾教授写 ...
- 吴裕雄--天生自然python机器学习:基于支持向量机SVM的手写数字识别
from numpy import * def img2vector(filename): returnVect = zeros((1,1024)) fr = open(filename) for i ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 机器学习——支持向量机SVM
前言 学习本章节前需要先学习: <机器学习--最优化问题:拉格朗日乘子法.KKT条件以及对偶问题> <机器学习--感知机> 1 摘要: 支持向量机(SVM)是一种二类分类模型, ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
随机推荐
- 【scikit-learn基础】--『预处理』之 标准化
数据的预处理是数据分析,或者机器学习训练前的重要步骤.通过数据预处理,可以 提高数据质量,处理数据的缺失值.异常值和重复值等问题,增加数据的准确性和可靠性 整合不同数据,数据的来源和结构可能多种多样, ...
- 接收json数据
1.导入坐标: <dependency> <groupId>com.fasterxml.jackson.core</groupId> <artifactId& ...
- 数字孪生系统为何需要将GIS系统进行融合?
数字孪生是一种通过数字模型实时仿真现实世界的技术,而GIS(地理信息系统)则是用于收集.存储.处理和展示地理数据的工具.将数字孪生系统与GIS系统进行融合,可以为各行业带来诸多优势和创新.那么数字孪生 ...
- 从零玩转七牛云之CDN-qiniuyunzhicdn
title: 从零玩转七牛云之CDN date: 2022-03-27 19:14:43.036 updated: 2022-04-10 14:13:27.322 url: https://www.y ...
- JavaFx 打包jar(六)
JavaFx 打包jar(六) JavaFX 从入门入门到入土系列 我们编写了不少javafx,那么如何打包成jar给用户呢?下面我给出比较全的打包方式. 打包jar 下面我给出比较全的打包方式. 1 ...
- MongoDB 安装、配置及详细使用教程
环境:win10 下载地址 :https://pan.baidu.com/s/1a0SwRv9er3HTewzcI8nWgQ 提取码:dyyx 下载后,将该文件夹放在C盘的根目录下,然后 ...
- 微信小程序本地测试报错 IllegalArgumentException
在微信小程序本地测试时出现 IllegalArgumentException 错误,解决方法将https换成http Note: further occurrences of HTTP request ...
- LeetCode DP篇(62、63、322、887)
62. 不同路径 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为"Start" ). 机器人每次只能向下或者向右移动一步.机器人试图达到网格的右下角(在下图中 ...
- 神经网络入门篇:深度学习和大脑的关联性(What does this have to do with the brain?)
深度学习和大脑的关联性 开始讲故事(手动狗头) 深度学习和大脑有什么关联性吗? 关联不大. 那么为什么会说深度学习和大脑相关呢? 当你在实现一个神经网络的时候,那些公式是你在做的东西,你会做前向传播. ...
- Prometheus配置Basic Auth进行安全防护,实现登录控制
本文分享自华为云社区<Prometheus配置Basic Auth进行安全防护,实现登录控制>,作者:可以交个朋友. 一.Prometheus Basic Auth 使用背景 在日常pro ...
