最近在做的项目中，使用querySelectorAll获取了同class名的元素后，绑定onmouseover事件和onmouseout后，多次在几个元素上移入移出操作时，控制台出现了报错的问题，最后解决方案时采用了getElementsBy系列的方法。

在查阅网络上的几篇相关的文章后，可以这样简单的解释两者的区别：

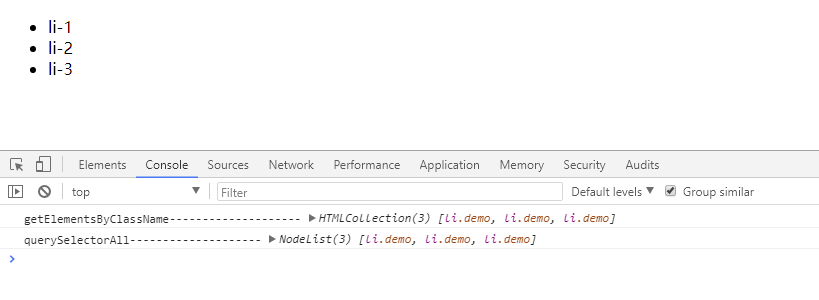
getElementsBy系列返回值是一个动态的HTMLCollection对象集合，每一次调用 li 都会重新对文档进行查询；

querySelector系列是一个静态的NodeList对象集合，它相当于是 li 集合的快照，对文档的任何操作都不会对其产生影响。

getElementsBy 系列方法相比querySelector系列的区别的更多相关文章

  1. querySelector系列方法相比 getElementsBy 系列方法有什么区别？

    querySelector 和  querySelectorAll 相比下面这些方法有什么区别? getElementsByTagName getElementsByClassName getElem ...

  2. ReactiveSwift源码解析(九) SignalProducerProtocol延展中的Start、Lift系列方法的代码实现

    上篇博客我们聊完SignalProducer结构体的基本实现后,我们接下来就聊一下SignalProducerProtocol延展中的start和lift系列方法.SignalProducer结构体的 ...

  3. querySelectorAll 方法相比 getElementsBy 系列方法区别

    最近有人问到querySelectorAll 方法相比 getElementsBy 系列方法区别,一时没想起来说些什么,今天查下文档,总结一下它们的区别,以便自己理解. 1. W3C 标准queryS ...

  4. getElementBy系列和querySelector系列的区别

    querySelector和querySelectorAll的用法和getElementBy大致一样,获取的时候带上符号,getElementBy获取的是元素的动态集合,querySelector获取 ...

  5. Java 集合系列 11 hashmap 和 hashtable 的区别

    java 集合系列目录: Java 集合系列 01 总体框架 Java 集合系列 02 Collection架构 Java 集合系列 03 ArrayList详细介绍(源码解析)和使用示例 Java ...

  6. 【形式化方法：VDM++系列】2.VDMTools环境的搭建

    接前文:http://www.cnblogs.com/Kassadin/p/3975853.html 上次讲了软件需求分析的演化过程,本次进入正题——VDM开发环境的搭建 (自从发现能打游戏以来,居然 ...

  7. 【形式化方法：VDM++系列】1.前言

    1.前言 今天开始上课学习软件需求分析与VDM++,经过一节课的学习,我又增长了见识. 软件需求工程在软件工程中处于十分核心的地位:需求分析的好坏直接决定软件工程的成败.这一点是我之前对需求工程的理解 ...

  8. Tree通用的系列方法列表-treepanel

    在项目中经常会用到Tree来显示数据进行操作.今天整理出来一系列操作Tree的方法.可供项目中方便调用.不用重复写代码,快速应用,通用性很强. Tree系列方法列表如下:主要针对的是ext.net中的 ...

  9. xorm -sum 系列方法实例

    求和数据可以使用Sum, SumInt, Sums 和 SumsInt 四个方法,Sums系列方法的参数为struct的指针并且成为查询条件. package main import ( " ...

随机推荐

  1. Bootstrap 网页1

    <!DOCTYPE html> <html> <head> <meta charset="utf-8" /> <title&g ...

  2. Spring boot与thymeleaf的集成

    # thymeleaf热部署 spring.thymeleaf.cache=false @Value("${spring.thymeleaf.cache}")          p ...

  3. proxy汇总-1

    1.apt-get的proxy 新建/etc/apt/apt.conf.d目录下新建10proxy文件,添加: Acquire::http::proxy"http://xx.xx.xx.xx ...

  4. python字符串的截取，查找

    1.字符串的截取 str = "123456" str[:3] = 123 str[1:3] = 23 str[0:-1] = 12345 里面的数字都是index索引,从第一个索 ...

  5. 开源实践分享：Ceph bluestore部署实践

    https://blog.51cto.com/99cloud/2119884 Ceph bluestore部署 首先为大家分享Ceph bluestore具体该如何部署,使用环境如下• 单节点• Ce ...

  6. DM9000驱动网卡编程

    DM9000数据发送编程: static int dm9000_start_xmit(struct sk_buff *skb, struct net_device *dev) { unsigned l ...

  7. Python每日一题 005

    任一个英文的纯文本文件,统计其中的单词出现的个数. 代码 # coding:utf-8 import re def get_word(filename): fp=open(filename," ...

  8. 《ArcGIS Runtime SDK for .NET开发笔记》 --Hello Word

    这里我们将创建第一个用于显示地图的APP. 1.新建一个WPF程序 首先我们打开Visual Studio,选择新建项目. 选择已安装——模板——Windows桌面——WPF应用程序  2.添加Run ...

  9. 81、Tensorflow实现LeNet-5模型，多层卷积层，识别mnist数据集

    ''' Created on 2017年4月22日 @author: weizhen ''' import os import tensorflow as tf import numpy as np ...

  10. 使用FTP服务

    ftp 占用20   21两个端口 安装vsftpd程序 键入命令    yum install vsftpd -y 清空默认的防火墙默认规则: [root@linuxprobe ~]# iptabl ...