牛顿法求极值及其Python实现

最初对于牛顿法，我本人是一脸懵的。其基本原理来源于高中知识。在如下图所示的曲线，我们需要求的是f(x)的极值：

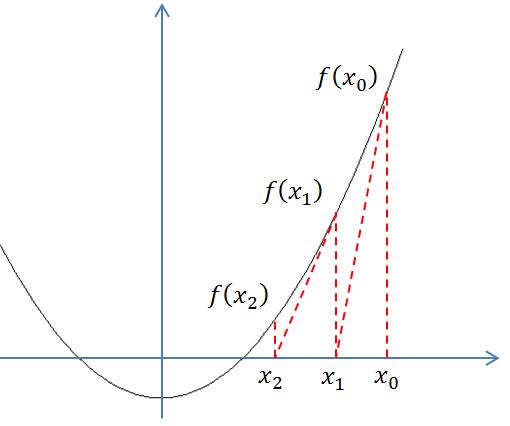
对于懵的原因，是忘记了高中所学的点斜式(Point Slope Form)，直接贴一张高中数学讲义：

因为我们一路沿着x轴去寻找解，所以迭代求f(x)=0的解得通用式为：

与梯度下降相比，牛顿法也同样是沿着曲线的斜率去寻找极值，但是不存在需要自定义learning rate的问题，因为alpha是由斜率来决定的。

牛顿法的python实现：

def newtons(f,df,x0,e):
    xn = float(x0)
    e_tmp = e+1
    loop = 1
    while e_tmp>e:
        print '########loop'+str(loop)
        k = df(xn)
        xm = f(xn)
        print 'xn='+str(xn)+',k='+str(k)+',y='+str(xm)
        q = xm/k
        xn = xn-q
        e_tmp = abs(0-f(xn))
        print 'new xn='+str(xn)+',e='+str(e_tmp)+',q='+str(q)
        loop=loop+1
    return xn

我们调用一下：

from Test1.newtonMethod import newtons
def f(x):
    return x**2+2*x

def df(x):
    return 2*x+2

x = newtons(f,df,3,0.01)
print 'the point you find is '+str(x)

运行结果如下：

########loop1
xn=3.0,k=8.0,y=15.0
new xn=1.125,e=3.515625,q=1.875
########loop2
xn=1.125,k=4.25,y=3.515625
new xn=0.297794117647,e=0.684269571799,q=0.827205882353
########loop3
xn=0.297794117647,k=2.59558823529,y=0.684269571799
new xn=0.0341661806366,e=0.0694996891724,q=0.26362793701
########loop4
xn=0.0341661806366,k=2.06833236127,y=0.0694996891724
new xn=0.000564381199631,e=0.0011290809254,q=0.0336017994369
the point you find is 0.000564381199631