10.1综合强化刷题 Day3 morning

　　　　　　　　　　　　　　　　　　　　　　　　竞赛时间：????年??月??日??:??-??:??

题目名称	a	b	c
名称	a	b	c
输入	a.in	b.in	c.in
输出	a.out	b.out	c.out
每个测试点时限	1s	1s	1s
内存限制	256MB	256MB	256MB
测试点数目	10	10	10
每个测试点分值	10	10	10
是否有部分分	无	无	无
题目类型	传统	传统	传统

a

【问题描述】

你是能看到第一题的 friends 呢。

——hja

怎么快速记单词呢？也许把单词分类再记单词是个不错的选择。何大爷给出了一种分单词的方法，何大爷认为两个单词是同一类的当这两个单词的各个字母的个数是一样的，如 dog 和 god。现在何大爷给了你 N个单词，问这里总共有多少类单词。

【输入格式】

第一行一个整数N代表单词的个数。接下来N行每行一个单词。

【输出格式】

一行一个整数代表答案。

【样例输入】

3

AABAC

CBAAA

AAABB

【样例输出】

2

本来打的是个70分的暴力，结果后面两个点A了，第8个点T了、、准是看本姑娘太可爱了、、

将近n^2枚举，判断一个字符是否与另一个字母相同，在比较的时候挨个字母的个数进行比较

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
bool flag;
];
],fa[N];
int find(int x)
{
    if(fa[x]==x) return x;
    return fa[x]=find(fa[x]);
}
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    n=read();ans=n;
    ;i<=n;i++) cin>>ch[i],l[i]=strlen(ch[i]);
//    sort()
    ;i<=n;i++)
     ;j<l[i];j++)
      sum[i][ch[i][j]-'A']++;
    ;i<=n;i++) fa[i]=i;
    ;i<=n;i++)
     ;j<=n;j++)
     {
        flag=false;
        ;k<;k++)
         if(sum[i][k]!=sum[j][k]) {flag=true; break;}
        if(!flag)
         if(find(i)!=find(j)) fa[j]=i,ans--;
     }
    printf("%d",ans);
    ;
}

考场90分代码

AC代码

将字符串转换成数字进行比较（在转换的时候我们要乘一个质数，乘质数重复的可能性很小），sort排序以后判断当前数是否与他后面的数相同，如果不同ans++

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 10010
using namespace std;
];
int n,l[N],ans,num[N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    n=read();
    ;i<=n;i++)
    {
        cin>>ch,l[i]=strlen(ch);
        sort(ch,ch+l[i]);
        ;j<l[i];j++)
         num[i]=num[i]*+ch[j]-;
    }
    sort(num+,num++n);
    ;i<n;i++)
     ]) ans++;
    printf();
    ;
}

AC代码

b

【问题描述】

你是能看到第二题的 friends 呢。

——laekov

长度为n 的铁丝，你可以将其分成若干段，并把每段都折成一个三角形。你还需要保证三角形的边长都是正整数并且三角形两两相似，问有多少种不同的分法。

【输入格式】

一行一个整数n 。

【输出格式】

一行一个整数代表答案对10⁹ + 7取模之后的值。

【样例输入 1

6

【样例输出 1】

2

【样例输入 2】

9

【样例输出 2】

6

【样例解释 2】

(1,1,1), (2,2,2); (2,2,2), (1,1,1)算两种方案。

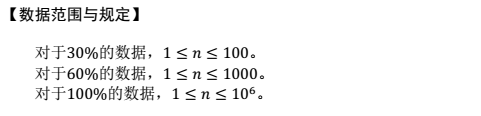
我们假设每一段的长度为Li，g=gcd(Li)；

我们用f[i]表示周长为i的能组成的三角形的个数，用sum[n/i]表示将n/i个单位（为什么是n/i个单位，因为现在三角形的周长为i，我们要将n分开，最小的周长单位为i，一共有n/i组这样的周长可以进行分配）分配给任意多个三角形的方案数，g[i]表示我们可以使用的三角形的周长。

我们对于最小的周长可以将它的三条边设为a,b,c，我们设a<=b<=c

接下来我们在处理的时候对b与c的大小关系进行分类讨论，

当b=c的时候

这样b的大小就在(g/3)（上取整）~(g-1)/2（下取整）之间，这样f[g]的大小即为f[g]=floor((g-1)/2）- ceil(g/3) +1

当b<c的时候

这种情况下所有的情况都可以由a，b，c-1的每一种方案转移过来但有一种除外：a+b=c，因为此时a，b，c-1 合法，a，b，c 不合法，这种情况为当g为偶数时，a+b+a+b=g，g=2*（a+b），所以有floor（g/4）个所以f[g]=f[g-1]+ （b&1）？ 0 ： -g/4

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1000001
#define mod 1000000007
using namespace std;
int n,ans,cnt,f[N],g[N],sum[N];
int read()
{
    ,f=; char ch=getchar();
    ;ch=getchar();}
    +ch-',ch=getchar();
    return x*f;
}

int main()
{
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    n=read();
    ;i<=n;i++)
    {
        f[i]=f[i-];
        f[i]=f[i]%mod+(i->>)%mod-ceil(i*)+;//设a<b<c，当b=c时，g=a+2b，那么b∈[ceil(g/3),floor((g-1)/2)]所以f[g]=floor((g-1)/2）- ceil(g/3) +1
        ==) f[i]=f[i]%mod-i/;//当i为偶数的时候，可能会形成a+b=c的这种情况，这是没有值的，g=a+b+c,g=2*（a+b），所以有floor（g/4）个
    }
    ;i*i<=n;i++)//找n的因子 ，处理出g为可以存在的三角形的周长
     )
     {
        g[++cnt]=i;
        if(i*i!=n) g[++cnt]=n/i;
     }
    sort(g+,g+cnt+);
    ;i<=cnt;i++)
     ;j<i;j++)
      ) f[g[i]]=(f[g[i]]%mod+(mod-f[g[j]])%mod)%mod;//然后因为要求三边长互质，所以枚举g的每个因数k，f[g]-=f[k]
    sum[]=;
    ;i<=n;i++) sum[i]=sum[i-],sum[i]=(sum[i]%mod+sum[i-]%mod)%mod;//把i个物品分成任意份的方案数=C（i-1,0）+C（i-1，1）+……+C（i-1，i-1）= 2^(i-1)
    ;i<=cnt;i++) ans=(ans%mod+1ll*sum[n/g[i]-]*f[g[i]]%mod)%mod;
    printf("%d",ans);
     ;
}

AC代码

c

【问题描述】

你是能看到第三题的 friends 呢。

——aoao

在小学的时候，我们都学过正视图和左视图。现在何大爷用一些小方块摆了一个图形，并给出了你这个图形的左视图和正视图。现在何大爷希望知道，在给定正视图和左视图的情况下，原来的立体图形有多少种可能的情况？

【输入格式】

第一行两个整数N ,M ，代表在左视图和正视图中分别有多少列。

第二行N个整数，代表在左视图中从左至右每一列的高度。

第三行M个整数，代表在正视图中从左至有每一列的高度。

【输出格式】

一行一个整数代表答案对10⁹ + 9取模之后的值。

【样例输入 1】

2 2

1 1

1 1

【样例输出 1】

7

【样例输入 2】

4 5

5 2 4 1

5 2 4 0 1

【样例输出 2】

429287

　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　距 NOIp2017 还剩 28 天

　　                             你可以做的事情还有很多，即使到最后一秒也不要放弃，因为不到结束的那一刻谁也不知道结果会怎样。