Curve 曲线 工具

　　　　最近研究了曲线绘制的工具，主要是2D方程的绘制。综合了许多工具，完成了一下两个脚本。

绘制的工具：

 using UnityEngine;
 using System.Collections;
 using UnityEngine.UI;

 public class Curve : MaskableGraphic
 {
     public Color color;
     public float m_LineWidth = ;
     [Range(, )]
     public int Acc = ;
     public System.Func<float, float> xConvert = x=>x;
     public System.Func<float, float> yConvert = y => y;
     public System.Func<float, float> MainFunc = f => f;
     protected override void OnPopulateMesh(VertexHelper vh)
     {
         var rect = this.rectTransform.rect;
         vh.Clear();
         Debug.Log(rect.xMin);
         Debug.Log(rect.xMax);
         Vector2 pos_first = new Vector2(rect.xMin, CalcY() * rect.height+rect.yMin);

         for (float x = rect.xMin + Acc; x < rect.xMax; x += Acc)
         {
             Vector2 pos = new Vector2(x, CalcY((x - rect.xMin) / rect.width) * rect.height+rect.yMin);
             var quad = GenerateQuad(pos_first, pos);

             vh.AddUIVertexQuad(quad);

             pos_first = pos;
         }

         Vector2 pos_last = new Vector2(rect.xMax, CalcY() * rect.height+rect.yMin);
         vh.AddUIVertexQuad(GenerateQuad(pos_first, pos_last));

         for (int i = ; i < vh.currentVertCount - ; i += )
         {
             vh.AddTriangle(i + , i + , i + );
             vh.AddTriangle(i + , i + , i + );
         }
         Debug.Log("PopulateMesh..." + vh.currentVertCount);
     }

     //根据曲线组件来计算Y
     //**** x 为 (x - rect.xMin) / rect.width)  所以范围 为 0~1
     //返回值 为y ，取值范围限定在 0~1；
     private float CalcY(float x)
     {
         return yConvert((MainFunc(xConvert(x))));
     }

     private UIVertex[] GenerateQuad(Vector2 pos1, Vector2 pos2)
     {
         float dis = Vector2.Distance(pos1, pos2);
         float y = m_LineWidth * 0.5f * (pos2.x - pos1.x) / dis;
         float x = m_LineWidth * 0.5f * (pos2.y - pos1.y) / dis;

         if (y <= )
             y = -y;
         else
             x = -x;

         UIVertex[] vertex = new UIVertex[];

         vertex[].position = new Vector3(pos1.x + x, pos1.y + y);
         vertex[].position = new Vector3(pos2.x + x, pos2.y + y);
         vertex[].position = new Vector3(pos2.x - x, pos2.y - y);
         vertex[].position = new Vector3(pos1.x - x, pos1.y - y);

         for (int i = ; i < vertex.Length; i++)
         {
             vertex[i].color = color;
         }

         return vertex;
     }
 }

控制脚本：

 using UnityEngine;
 using System.Collections;
 using System;
 [RequireComponent(typeof(Curve))]
 public class CurveItem : MonoBehaviour {
     private Curve curve;
     private Vector2[] posArray;

     //绘制谱图x 最小值
     [Header("绘制谱图x 最小值")]
     public float xMin;
     //绘制谱图 x 最大值
     [Header("绘制谱图x 最大值")]
     public float xMax;
     //绘制 谱图 y 最小值
     [Header("绘制谱图y 最小值")]
     public float yMin;
     //绘制谱图 y 最大值
     [Header("绘制谱图y 最大值")]
     public float yMax;
     [Header("绘制谱图取样间隔")]
     public float delta;
     // Use this for initialization
     void Start () {
         curve = this.GetComponentInChildren<Curve>();
     }

     #region 主要方法

     public void ShowPutu(Func<float, float> func)
     {
         //    DrawLine(LineDrawer.GetSampleArray(func, xMin, xMax, delta));
         curve.MainFunc = func;
         curve.xConvert = MathTool.GetLinear(, xMin, , xMax);
         curve.yConvert = MathTool.GetLinear(yMin, , yMax, 1f);
         curve.enabled = false;
         curve.enabled = true;
     }

     #endregion

     #region Test

     private Func<float, float> func = x=>x*x;

     [ContextMenu("谱图")]
     private void Test()
     {
         ShowPutu(func);
     }

     #endregion
 }

Math工具

     //获取线性方程
     public static Func<float, float> GetLinear(float x0, float y0, float x1, float y1)
     {
         Func<float, float> linear = x =>
         {
             float a = (y1 - y0) / (x1 - x0);
             return x*a+y0-x0*a;
         };
         return linear;
     }

调用以下方法即可。

ShowPutu(Func<float, float> func)

将两个脚本都挂载在Canvas下的一个空物体上。

演示 x=>x*x：

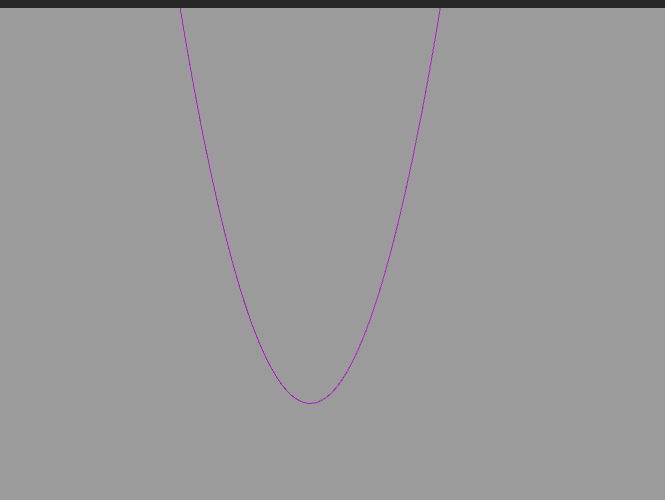
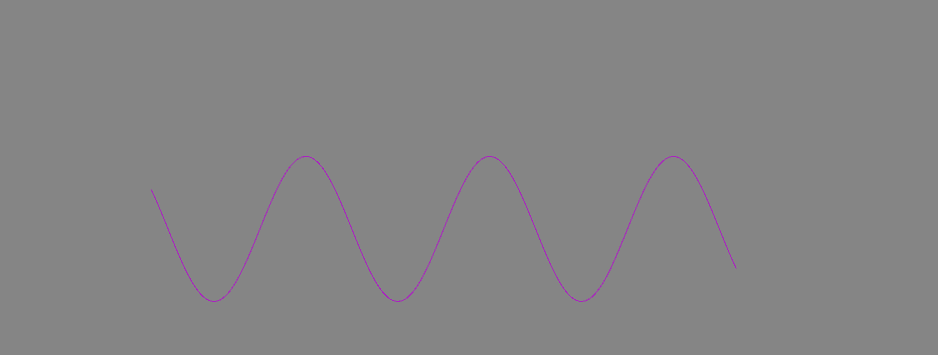
演示 x=>Mathf.Asin(x)：