【题解】 2月19日厦门双十中学NOIP2014模拟D2 T1 采药人的切题规则

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Made by 退役的OIer

第一次写博客,写得不好 or 不清楚的可以在下方留言,我会尽量改进的!

好啦~~~回到正题,题面见传送门

【问题描述】

　　采药人最近在认真切题，但回旋的转盘时常在眼前浮现，旧日的美好时光总把他带回那个无忧无虑的押忍战斗应援团的时代。于是他在切题的时候也按照这样的规则以怀念旧时光。

　　规则是这样的：采药人手头有 n 道题，他会将其按 1 到 n 的顺序绕成一个环，他会从 1开始按照 1 到 n 顺序每隔 p 道没写过的写一题，直到这些题都写完了。他想知道这些题中第 k 个被他切掉的题是第几题？

　　如有 7 道题，采药人每隔 3 道写一题。那么他写题的顺序是 3 6 2 7 5 1 4。

【输入格式】

第一行，一个整数 t，表示数据组数

接下来 t 行，每行三个正整数 n,p,k，意义如题目所述

【输出格式】

t 行，每行一个整数，表示答案

【输入输出样例】

rule.in

7 3 7

rule.out

【数据规模】

对于 20%,k<=n<=1000,p<=100

对于 40%,k<=n<=10000,p<=1000

对于另外 20%,k<=n<=1000000000,p<=2

对于 100%,t<=10,k<=n<=10^14,p<=10000

solution:

　　首先我们可以看出这就是Joseph问题（如果不会请移步至Joseph问题）

最最基础的算法就是模拟啦~~~

数p道题就切掉当前这个,重复k次,我们当然可以使用循环链表模拟这个过程(很形象的)

部分代码如下:

void pre()

{

    FOR(i,,n)

    {

        l[i]=(i==)?n:i-;

        r[i]=(i==n)?:i+;

    }

    return;

}

void del(int x)//在链表中删除x(即把x两边的连起来)

{

    r[l[x]]=r[x];

    l[r[x]]=l[x];

    return;

}

//在main中

int pos=n;

while(k-->)

{

    FOR(i,,p) pos=r[pos];

    del(pos);

}

printf("%d",pos);

哈哈,是不是很简单?

然而,仔细一想,整个算法时间复杂度为O(pk)

emmm....显然炸得裂开

我们急需寻找一个更为高效的算法

递推!

我们发现,一个队列进行一次切题操作后,长度会减小1,而队列开头到切掉的题的下一个

即可以从此处重新编号1~(n-1),相当于对当前队列编号整体减p

(自己推一推,模拟 切一道题 的过程)

假设f[i][j]为队列长度为 i 时 , 切掉的第 j 道题的编号

则有以下递推式:

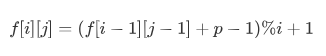
初态即

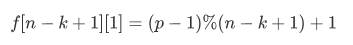
又可以发现,f数组没有必要,只用一个变量pos即可

那么代码就出来了:

//在main中

int pos=(p-)%(n-k+)+;

FOR(i,n-k+,n)

{

    pos=(pos+p-)%i+;

}

printf("%d",pos);

分析一波发现,算法时间复杂度降到了O(k)

wow~~~优(yiu)秀(xiu)

欣喜地看看数据范围, ?@#(*%&@#!

k<=n<=10^14

这说明我们需要更~~~~~~~~高效的算法!

???(仔细想想怎么优化,想完再往下看)

就一个小优化即可:乘法加速

用乘法加速加法运算(是不是很简单)

(不对呀,这里有取模,怎么加速???)

很容易发现,取模并不是每次都有改变,就是说取模把加法分成了若干小段,每个小段中pos是连加的

每次 i 增加 1 时, pos 增加 p(是不是很像追及问题?)

那么每段中, i 就会增加 tmp, 其中

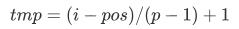
这样就很好办了~~~

再就不多说了,见完整代码

#include<cstdio>

#define ll long long

#define rll register ll

ll n,p,k,len,pos;

int T;

int main()

{

    scanf("%d",&T);

    while(T-->)

    {

        scanf("%lld%lld%lld",&n,&p,&k);

        if(p==) printf("%lld\n",k);//注意特判p==1的时候

        else

        {

            len=n-k+;pos=(p-)%len+;

            for(rll tmp();len+tmp<=n;tmp=(len-pos)/(p-)+)

                pos=(pos+tmp*p-)%(len+=tmp)+;

            printf("%lld\n",(pos+(n-len)*p-)%n+);

        }

    }

    return ;

}

是不是很简单?

复杂度也很简单,O(T * F(k) )(其中F(k)为关于k的函数,值很小,可近似为log(k))

愉快地 切一道题 啦~~~

最后,

感谢 P.Y.Y 提供的官方题解平台~~~

感谢各位 巨佬&&神犇 的支持与鼓励~~~