A task in a suit and a tie:paraphrase generation with semantic augmentation解读

1.该算法核心:在seq2seq模型的编码器中增加语义的frame 和 roles

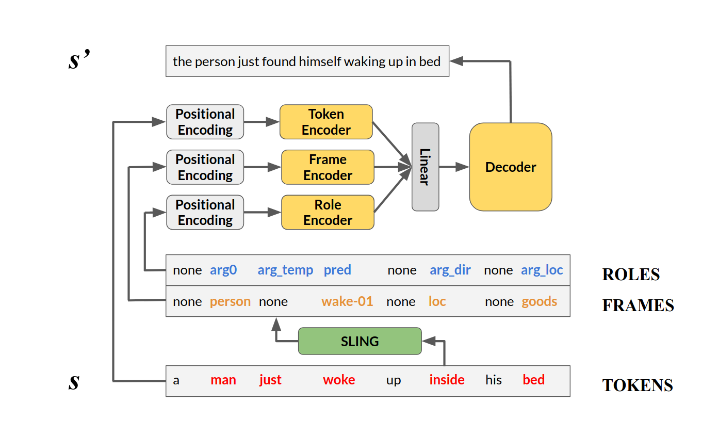
2.上图为算法整个流程：

1).首先输入一句话s，SLING会使用frame和role label注释输入语句s，然后将这些label转换成token，因此会有三个对齐向量：tokens,frames,roles；（使用SLING目的：预测结构语义表示，生成表示输入文本含义的框架图表示frame graph representing）

2).每个向量会有一个独立的channel,每个channel中有一个独立的Transformer编码器，每个编码器会输出一个向量，一共有三个输出向量(Transformer:使用位置信息进行并行编码，避免token-by-token编码；编码器的构成要素是多头注意力层，之后是一个前馈层，其中都包含剩余的链路和层规范)

3).步骤2生成的三个向量，会经过一个线性层，该层接受三个向量，输出一个向量，是输入的线性组合（我理解的）

4).将步骤3中输出的一个向量，放入解码器中，最终会输出不改变s原意的一句话。