【bzoj2521】[Shoi2010]最小生成树 网络流最小割

题目描述

Secsa最近对最小生成树问题特别感兴趣。他已经知道如果要去求出一个n个点、m条边的无向图的最小生成树有一个Krustal算法和另一个Prim的算法。另外，他还知道，某一个图可能有多种不同的最小生成树。例如，下面图 3中所示的都是图 2中的无向图的最小生成树：

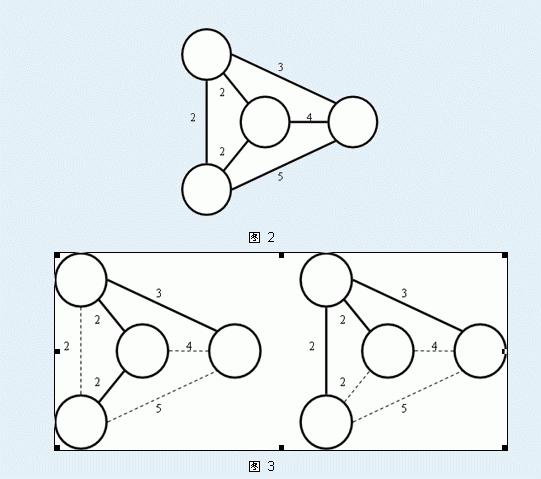
当然啦，这些都不是今天需要你解决的问题。Secsa想知道对于某一条无向图中的边AB，至少需要多少代价可以保证AB边在这个无向图的最小生成树中。为了使得AB边一定在最小生成树中，你可以对这个无向图进行操作，一次单独的操作是指：先选择一条图中的边 P1P2，再把图中除了这条边以外的边，每一条的权值都减少1。如图 4所示就是一次这样的操作：

输入

输入文件的第一行有3个正整数n、m、Lab分别表示无向图中的点数、边数、必须要在最小生成树中出现的AB边的标号。

接下来m行依次描述标号为1,2,3…m的无向边，每行描述一条边。每个描述包含3个整数x、y、d，表示这条边连接着标号为x、y的点，且这条边的权值为d。

输入文件保证1<=x,y<=N,x不等于y,且输入数据保证这个无向图一定是一个连通图。

输出

输出文件只有一行，这行只有一个整数，即，使得标号为Lab边一定出现最小生成树中的最少操作次数。

样例输入

4 6 1
1 2 2
1 3 2
1 4 3
2 3 2
2 4 4
3 4 5

样例输出

1

---

题解

网络流最小割

除了这条边以外其它边都-1，相当于其它边不变，这条边+1。

然后考虑Kruscal求最小生成树的方法，一条边一定出现在最小生成树上，等价于所有边权小于等于它的边不能使得这两个端点连通。

于是转化为最小割问题。

对于每条长度小于等于给定的边，连容量为 给定长度-当前长度+1 的边，然后跑最小割即可。

#include <queue>
#include <cstdio>
#include <cstring>
#define N 510
#define K 810
#define M 100010
using namespace std;
queue<int> q;
int x[K] , y[K] , z[K] , head[N] , to[M] , val[M] , next[M] , cnt = 1 , s , t , dis[N];
void add(int x , int y , int z)
{
    to[++cnt] = y , val[cnt] = z , next[cnt] = head[x] , head[x] = cnt;
    to[++cnt] = x , val[cnt] = z , next[cnt] = head[y] , head[y] = cnt;
}
bool bfs()
{
    int x , i;
    memset(dis , 0 , sizeof(dis));
    while(!q.empty()) q.pop();
    dis[s] = 1 , q.push(s);
    while(!q.empty())
    {
        x = q.front() , q.pop();
        for(i = head[x] ; i ; i = next[i])
        {
            if(val[i] && !dis[to[i]])
            {
                dis[to[i]] = dis[x] + 1;
                if(to[i] == t) return 1;
                q.push(to[i]);
            }
        }
    }
    return 0;
}
int dinic(int x , int low)
{
    if(x == t) return low;
    int temp = low , i , k;
    for(i = head[x] ; i ; i = next[i])
    {
        if(val[i] && dis[to[i]] == dis[x] + 1)
        {
            k = dinic(to[i] , min(temp , val[i]));
            if(!k) dis[to[i]] = 0;
            val[i] -= k , val[i ^ 1] += k;
            if(!(temp -= k)) break;
        }
    }
    return low - temp;
}
int main()
{
    int n , m , p , i , ans = 0;
    scanf("%d%d%d" , &n , &m , &p);
    for(i = 1 ; i <= m ; i ++ ) scanf("%d%d%d" , &x[i] , &y[i] , &z[i]);
    s = x[p] , t = y[p];
    for(i = 1 ; i <= m ; i ++ )
        if(i != p && z[i] <= z[p])
            add(x[i] , y[i] , z[p] - z[i] + 1);
    while(bfs()) ans += dinic(s , 1 << 30);
    printf("%d\n" , ans);
    return 0;
}