广义线性模型（Generalized Linear Models）

前面的文章已经介绍了一个回归和一个分类的例子。在逻辑回归模型中我们假设：

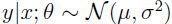
在分类问题中我们假设：

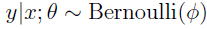
他们都是广义线性模型中的一个例子，在理解广义线性模型之前需要先理解指数分布族。

指数分布族（The Exponential Family）

如果一个分布可以用如下公式表达，那么这个分布就属于指数分布族：

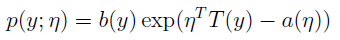
公式中y是随机变量；h(x)称为基础度量值（base measure）；

η称为分布的自然参数（natural parameter），也称为标准参数（canonical parameter）；

T(y)称为充分统计量，通常T(y)=y；

a(η)称为对数分割函数（log partition function）；

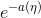本质上是一个归一化常数，确保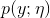概率和为1。

当T(y)被固定时，a(η)、b(y)就定义了一个以η为参数的一个指数分布。我们变化η就得到这个分布的不同分布。

伯努利分布属于指数分布族。伯努利分布均值为φ，写为Bernoulli(φ)，是一个二值分布，y ∈ {0, 1}。所以p(y = 1; φ) = φ; p(y = 0; φ) = 1 − φ。当我们变化φ就得到了不同均值的伯努利分布。伯努利分布表达式转化为指数分布族表达式过程如下：

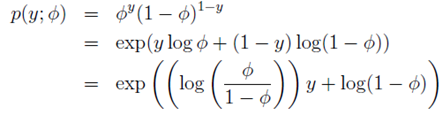
其中，

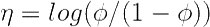
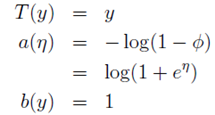
再举一个高斯分布的例子，高斯分布也属于指数分布族。由高斯分布可以推导出线性模型（推导过程将在EM算法中讲解），由线型模型的假设函数可以得知，高斯分布的方差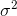与假设函数无关，因而为了计算简便，我们设方差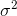=1。高斯分布转化为指数分布族形式的推导过程如下：

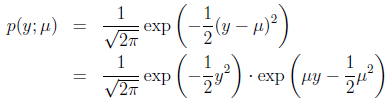
其中

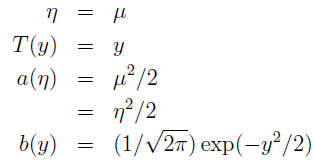
许多其他分部也属于指数分布族，例如：伯努利分布（Bernoulli）、高斯分布（Gaussian）、多项式分布（Multinomial）、泊松分布（Poisson）、伽马分布（Gamma）、指数分布（Exponential）、β分布、Dirichlet分布、Wishart分布。

构建广义线性模型（Constructing GLMs）

在分类和回归问题中，我们通过构建一个关于x的模型来预测y。这种问题可以利用广义线性模型（Generalized linear models，GMLs）来解决。构建广义线性模型我们基于三个假设，也可以理解为我们基于三个设计决策，这三个决策帮助我们构建广义线性模型：

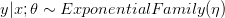1. ,假设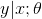满足一个以为参数的指数分布。例如，给定了输入x和参数θ，那么可以构建y关于η的表达式。
2. 给定x，我们的目标是要确定T(y)，即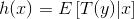。大多数情况下T(y)=y，那么我们实际上要确定的是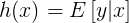。即给定x，假设我们的目标函数是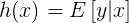。（在逻辑回归中期望值是，因此目标函数h是φ；在线性回归中期望值是μ，而高斯分布中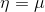，因此线性回归中目标函数）。
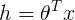3. 假设自然参数η和x是线性相关，即假设：

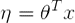
假设有一个预测问题：基于特征商店促销活动、最近的广告、天气、星期几等特征x，来预测商店在任一小时内的顾客数目y。

根据概率知识可知，x、y符合泊松分布。泊松分布属于指数分布族，我们可以利用上面的3个假设，构建一个广义线性模型来进行构建预测模型。

GLMs构建最小二乘模型

线性回归中的优化目标y（损失函数）是由最小二乘法得到的，可以使用广义线性模型构建最小二乘模型。三个假设：

1. 最小二乘法得到的目标变量y是一个连续值，我们假设给定x下y的分布符合高斯分布。假设1中的ExponentialFamily(η)就是高斯分布。
2. 在高斯分布中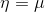，目标函数
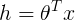
3. 假设：

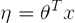
推导过程如下

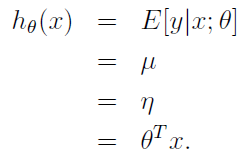
第一步变换根据假设2：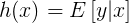

第二步变换根据y|x; θ ∼ N(μ, σ2)，高斯分布的期望值是μ

第三步根据假设1：高斯分布中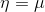

第四步根据假设3：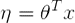

现在已经使用广义线性模型构建出了最小二乘模型，接下来的工作就是利用梯度下降、牛顿方法来求解θ。梯度下降、牛顿方法的内容请参考之前的讲义。

GLMs构建逻辑回归

逻辑回归可以用于解决二分类问题，而分类问题目标函数y是二值的离散值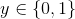，。根据统计知识，二分类问题可以选择伯努利分布来构建模型。

在伯努利分布的指数分布族表达式中我们已知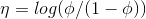：，从而得到。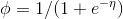

构建广义线性模型的三个假设：

1. 假设符合伯努利分布，
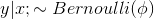
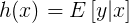2. ，伯努利分布中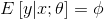
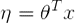
3. 

推导过程如下：

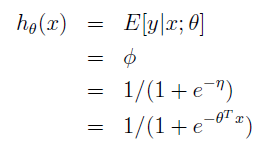
同最小二乘模型一样，接下来的工作就由梯度下降或牛顿方法来完成。

注意一下上面的推到结果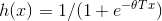，回忆一下，在逻辑回归中，我们选用Sigmoid函数。

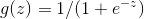之所以在逻辑回归中选用这个g(z)作为Sigmoid函数是由一套理论作支持的，这个理论便是广义线性模型。

出处：http://www.cnblogs.com/BYRans/