力扣74(java&python)-搜索二维矩阵（中等）

题目：

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

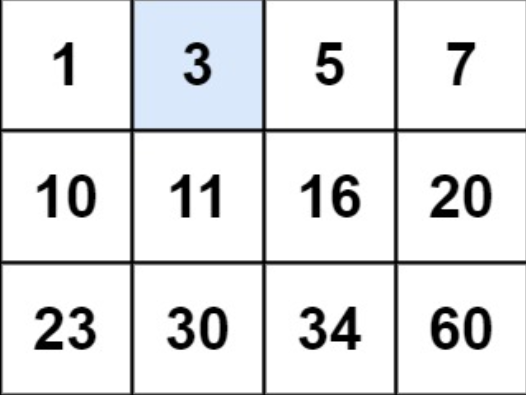
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3

输出：true

示例 2：

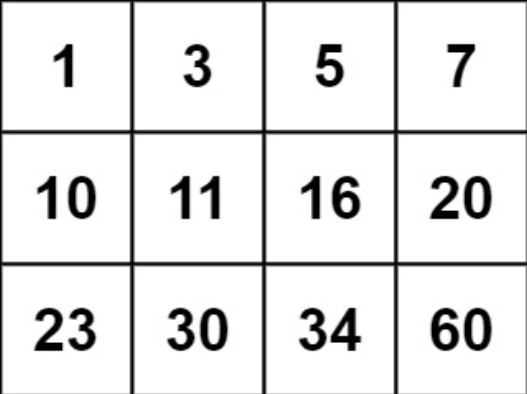
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13

输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10⁴ <= matrix[i][j], target <= 10⁴

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

【两次二分】

根据题目意思，每一行从上到下是升序的，每一列从上到下都是升序的，这样的话就可以运用两次二分查找，先找到合适的行，再找到合适的列。

• 第一次二分：从第0列中的所有行开始找，先聚焦target在哪个具体的行row；
• 第二次二分：在找到行的基础上，去找到合适的列col，从而就能确定出target是否在二维矩阵中。

java代码：

 1 class Solution {
 2     public boolean searchMatrix(int[][] matrix, int target) {
 4         int m = matrix.length, n = matrix[0].length;
 5         //第一次二分先找到行号
 6         int left = 0, right = m - 1;
 7         while (left < right){
 8             int mid = left + (right - left + 1) / 2;
 9             if (target >= matrix[mid][0]){
10                 left = mid;
11             }else{
12                 right = mid - 1;
13             }
14         }
15         //循环结束时：left > right
16         int row = right;
17         if (matrix[row][0] > target) return false;
18         //第二次二分找到列
19         left = 0; right = n - 1;
20         while (left < right){
21             int mid = left + (right - left) / 2;
22             if (target == matrix[row][mid]) return true;
23             if (target > matrix[row][mid]){
24                left = mid + 1;
25             }else {
26                right = mid;
27             }
28         }
29         int col = right;
30         return matrix[row][col] == target;
31     }
32 }

 python3代码：

 1 class Solution:
 2     def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
 3         m, n = len(matrix), len(matrix[0])
 4         left, right = 0, m - 1
 5         while left <= right:
 6             mid = left + (right - left) // 2
 7             if target > matrix[mid][0]:
 8                 left = mid + 1
 9             elif target < matrix[mid][0]:
10                 right = mid - 1
11             else:
12                 return True
13         row = right
14         left, right = 0, n-1
15         while left <= right:
16             mid = left + (right - left) // 2
17             if target > matrix[row][mid]:
18                 left = mid + 1
19             elif target < matrix[row][mid]:
20                 right  = mid - 1
21             else:
22                 return True
23         return False

 【直接遍历】

遍历查找每个位置，看target是否出现。

 java代码：

 1 class Solution {
 2     public boolean searchMatrix(int[][] matrix, int target) {
 3         int m = matrix.length, n = matrix[0].length;
 4         for (int i = 0; i < m; i++){
 5             for (int j = 0; j < n; j++){
 6                 if (matrix[i][j] == target){
 7                     return true;
 8                 }
 9             }
10         }
11         return false;
12     }
13 }

 python代码：

1 class Solution:
2     def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
3         m, n = len(matrix), len(matrix[0])
4         for i in range(m):
5             for j in range(n):
6                 if matrix[i][j] == target:
7                     return True
8         return False