BZOJ 1143: [CTSC2008]祭祀river（二分图最大点独立集）

http://www.lydsy.com/JudgeOnline/problem.php?id=1143

题意：

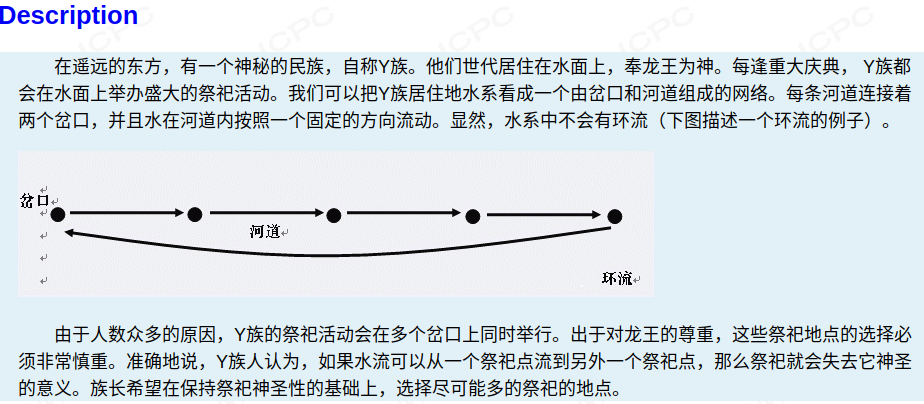
思路：

二分图最大点独立集，首先用floyd判断一下可达情况。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;

 int n,m,tot;
 int mp[][],mark[],head[];
 bool vis[];

 struct node
 {
     int v,next;
 }e[];

 void addEdge(int u,int v)
 {
     e[tot].v = v;
     e[tot].next = head[u];
     head[u] = tot++;
 }

 void floyd()
 {
     for(int k=;k<=n;k++)
     for(int i=;i<=n;i++)
     for(int j=;j<=n;j++)
         mp[i][j] = mp[i][j]||(mp[i][k]&&mp[k][j]);
 }

 bool match(int u)
 {
     for(int i=head[u];i!=-;i=e[i].next)
     {
         int v = e[i].v;
         if(!vis[v])
         {
             vis[v] = true;
             if(mark[v]==- || match(mark[v]))
             {
                 mark[v] = u;
                 return true;
             }
         }
     }
     return false;
 }

 int main()
 {
     tot = ;
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     for(int i=;i<m;i++)
     {
         int u,v;
         scanf("%d%d",&u,&v);
         mp[u][v] = ;
     }
     floyd();
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=n;j++)
         {
             if(mp[i][j]) addEdge(i,j);
         }
     }
     int sum = ;
     memset(mark,-,sizeof(mark));
     for(int i=;i<=n;i++)
     {
         memset(vis,,sizeof(vis));
         if(match(i))  sum++;
     }
     printf("%d\n",n-sum);
 }