轮廓线DP
轮廓线DP
刚刚学了轮廓线DP,想了好久才懂。
我的理解就是用一条线的状态去更新另一条线的状态,然后将格子填满。
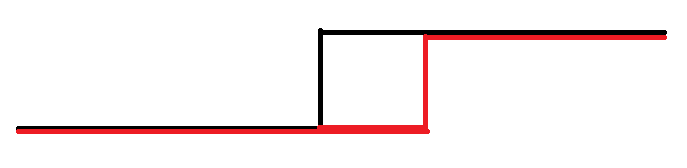
图中正方形即是要填东西(根据题意)的格子,红线的状态是由黑线转移过来的。
对于每一条线都有一个自己的状态(一个二进制数,先不用看1和0是啥意思),如下图。
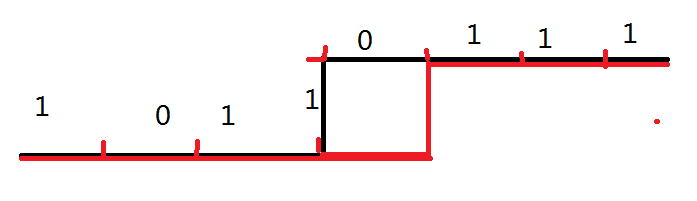
图中黑线的状态即是11101101(最左边的是二进制位第零位),编号从左往右为1,2,3,4,5,6,7,8。
具体一点,我们上例题。
题目大意:给你一个\(n*m\)\((1 <= n,m <= 100)\)的网格,让你在网格里填上长度不小于2的线段,问有多少种情况,对结果%\(1e9 + 7\)。
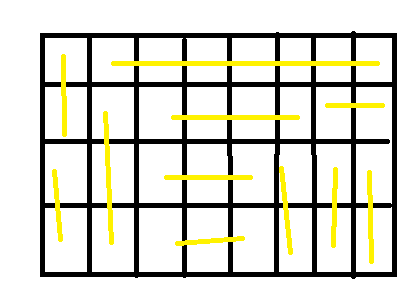
这是某一种情况。
现在我们轮廓线上的1和0就有意义了:如果竖着的这条线上的数为1的话,那么这个格子必须画一条横线(图一);如果横着的这条线上的数为1的话,那么这个格子必须画一条竖线(图二);我们发现,横线和竖线上不能同时为1,这是冲突的;如果横线和竖线上都为0,那么这个格子里话横线竖线都可以。
(不会画图,丑死了)
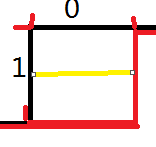 (图一)
(图一)
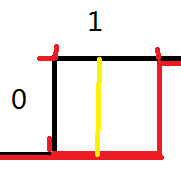 (图二)
(图二)
下面为了好打,把图一定义为(1, 0),图二定义为(0,1)。\(a[]\)是二进制数,\(i\)是下标:(\(a[i - 1]\), \(a[i]\))
对于一个格子,它上面的黑线有三种情况:(1, 0),(0, 1),(0, 0)。然后我们考虑怎么将黑线的状态转移到红线。
<1> 当黑线为(1,0)时,红线可以转移到的状态有:(0,1),(0,0)。(其他位上二进制数都一样)
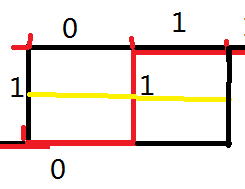

<2> 当黑线为(0,1)时,红线可以转移到的状态有:(1,0),(0,0)。
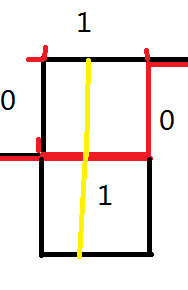
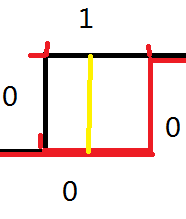
<3> 当黑线为(0,0)时,红线可以转移到的状态有:(0,1),(1,0)。(差不多,就不画了)
像这样一直转移下去,填完\(n*m\)个格子,就可以得到所有的方案。
我们考虑开一个二维\(unordered\) _ \(map\),\(unordered\)_\(map<int , long long> dp[2]\);\(dp[0,1][x] = val\),第一维是个滚动数组,第二维\(x\)是这条轮廓线的状态,\(val\)是这条线填完对应的那个格子后合法的方案数。
为啥用\(unordered\)\(map\),而不用\(map\)呢?\(map\): 该类型的搜索时间复杂度为\(O(logn)\) ;\(unordered_map\) : 搜索时间复杂度\(O(1)\)为平均时间,最坏情况下的时间复杂度为\(O(n)\);
#include <iostream>
#include <cstdio>
#include <unordered_map>
using namespace std;
const int p = 1e9 + 7;
int n, m;
void work(int n, int m) {
unordered_map <int, long long> dp[2];
int now = 0, nxt = 1;
dp[now][0] = 1;
for(int i = 1;i <= n; i++) {
for(int j = 1;j <= m; j++) {
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
int u = (nowst >> j) & 1, l = (nowst >> (j - 1)) & 1;
if(u == 0 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 1 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 0 && l == 1) {
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
}
swap(now, nxt);
}
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
if((nowst >> m) ^ 1) dp[nxt][nowst << 1] = nowval;
}
swap(now, nxt);
}
printf("%d", dp[now][0]);
}
int main() {
scanf("%d %d", &n, &m);
work(n, m);
return 0;
}
我也是刚学,哪说的不对的还希望大佬指出。
轮廓线DP的更多相关文章
- 轮廓线DP POJ3254 && BZOJ 1087
补了一发轮廓线DP,发现完全没有必要从右往左设置状态,自然一点: 5 6 7 8 9 1 2 3 4 如此设置轮廓线标号,转移的时候直接把当前j位改成0或者1就行了.注意多记录些信息对简化代码是很有帮 ...
- HDU4804 Campus Design 轮廓线dp
跟上面那篇轮廓线dp是一样的,但是多了两个条件,一个是在原图上可能有些点是不能放的(即障碍),所以转移的时候要多一个判断color[i][j]是不是等于1什么的,另外一个是我们可以有多的1*1的骨牌, ...
- POJ2411 Mondriaan's Dream 轮廓线dp
第一道轮廓线dp,因为不会轮廓线dp我们在南京区域赛的时候没有拿到银,可见知识点的欠缺是我薄弱的环节. 题目就是要你用1*2的多米诺骨排填充一个大小n*m(n,m<=11)的棋盘,问填满它有多少 ...
- UVA - 11270 轮廓线DP
其实这题还能用状压DP解决,可是时间达到2000ms只能过掉POJ2411.状压DP解法详见状压DP解POJ2411 贴上POJ2411AC代码 : 2000ms 时间复杂度h*w*(2^w)*(2^ ...
- [UOJ422][集训队作业2018]小Z的礼物——轮廓线DP+min-max容斥
题目链接: [集训队作业2018]小Z的礼物 题目要求的就是最后一个喜欢的物品的期望得到时间. 根据$min-max$容斥可以知道$E(max(S))=\sum\limits_{T\subseteq ...
- 【UOJ#422】【集训队作业2018】小Z的礼物(min-max容斥,轮廓线dp)
[UOJ#422][集训队作业2018]小Z的礼物(min-max容斥,轮廓线dp) 题面 UOJ 题解 毒瘤xzy,怎么能搬这种题当做WC模拟题QwQ 一开始开错题了,根本就不会做. 后来发现是每次 ...
- BZOJ.4572.[SCOI2016]围棋(轮廓线DP)
BZOJ 洛谷 \(Description\) 给定\(n,m,c\).\(Q\)次询问,每次询问给定\(2*c\)的模板串,求它在多少个\(n*m\)的棋盘中出现过.棋盘的每个格子有三种状态. \( ...
- 4572: [Scoi2016]围棋 轮廓线DP KMP
国际惯例的题面:这种题目显然DP了,看到M这么小显然要状压.然后就是具体怎么DP的问题.首先我们可以暴力状压上一行状态,然后逐行转移.复杂度n*3^m+3^(m*2),显然过不去. 考虑状态的特殊性, ...
- Solid Dominoes Tilings (轮廓线dp打表 + 容器)
第一步先打一个表,就是利用轮廓线DP去打一个没有管有没有分界线组合数量的表 #include<bits/stdc++.h> using namespace std; ; <<; ...
- HDU 4802 && HDU 4803 贪心,高精 && HDU 4804 轮廓线dp && HDU 4805 计算几何 && HDU 4811 (13南京区域赛现场赛 题目重演A,B,C,D,J)
A.GPA(HDU4802): 给你一些字符串对应的权重,求加权平均,如果是N,P不计入统计 GPA Time Limit: 2000/1000 MS (Java/Others) Memory ...
随机推荐
- json-lib无法下载
maven无法下载json-lib 配置一下这个 <classifier>jdk15</classifier> 因为远程提供了两个
- 【BZOJ3307】雨天的尾巴 题解(树链剖分+树上差分)
题目链接 题目大意:给定一颗含有$n$个结点的树,每次选择两个结点$x$和$y$,对从$x$到$y$的路径上发放一带$z$类型的物品.问完成所有操作后每个结点发放最多的时哪种物品. 普通的树链剖分貌似 ...
- mybatis中的延迟查询思想
1.一对一延迟加载 延迟加载: 就是在需要用到数据时才进行加载,不需要用到数据时就不加载数据.延迟加载也称懒加载. 好处:先从单表查询,需要时再从关联表去关联查询,大大提高数据库性能,因为查询单表要比 ...
- 家庭记账本APP开发准备(二)
今天学习了选项卡,为记账本的分类做了准备.主登录界面进行了优化,但仍未实现各个组件之间的跳转. 选项卡 activity_main.xml <?xml version="1.0&quo ...
- Nginx.conf参数配置详解
Nginx的配置文件nginx.conf配置详解如下: user nginx nginx; #Nginx用户及组:用户 组.window下不指定 worker_processes 8; #工作进程:数 ...
- 【工具】之001-CentOS7 最小化安装配置
写在前面 我很懒,,,不想敲一个命令一个命令敲... "偷懒是有前提的,不是之前,就是之后." 简述 CentOS 7 最小化安装版本:CentOS-7-x86_64-Minima ...
- ~/.ssh/目录找不到解决方法
执行 cd ~/.ssh发现.ssh目录找不到 原因是因为没有用root用户ssh登录过,执行一下ssh操作就会自动生成了
- [学习笔记] Numpy基础 系统学习
[学习笔记] Numpy基础 上专业选修<数据分析程序设计>课程,老师串讲了Numpy基础,边听边用jupyter敲了下--理解+笔记. 老师讲的很全很系统,有些点没有记录,在PPT里就不 ...
- CSS动画实例:图文切换
先准备好一张图片,在页面中放置一个类名为container的层作为图文容器,在该层中再定义两个层:一个类名为image-box的层放置图片,一个类名为text-desc的层放置文本描述,HTML代码描 ...
- 如何使 pdf 文件在浏览器里面直接下载而不是打开
前言 在做需求过程中我们大概率会遇到在浏览器中下载文件的需求,如果仅仅是这个要求的话很简单,有如下两种解决方式. 第一种是通过 window 对象的 open 方法进行操作,将文件 url 直接在浏览 ...
