【JZOJ】3490. 旅游题解报告

题目

---

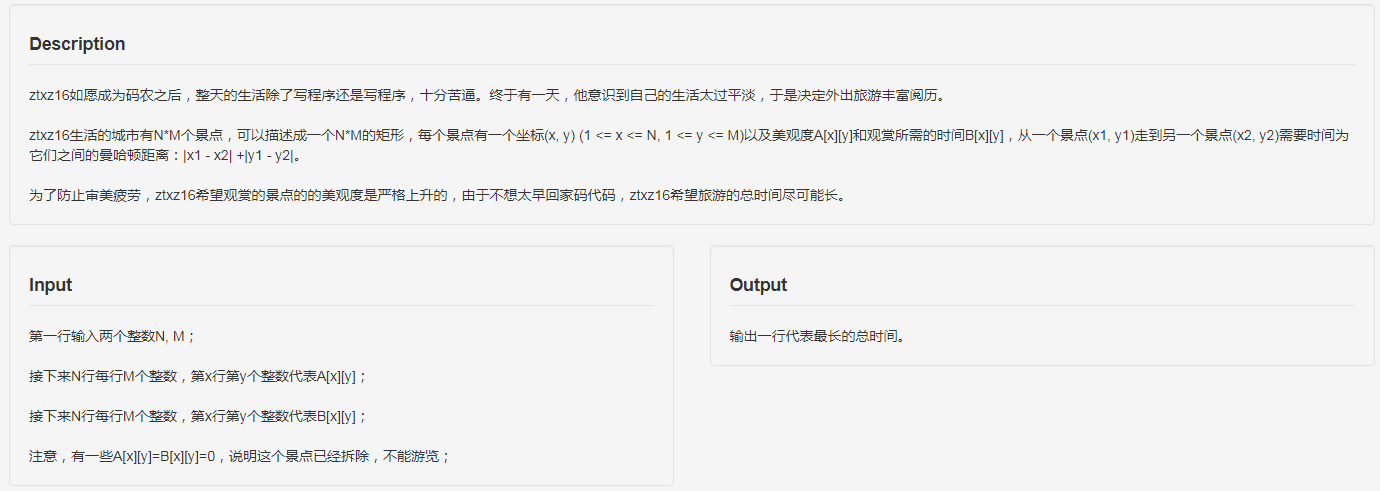
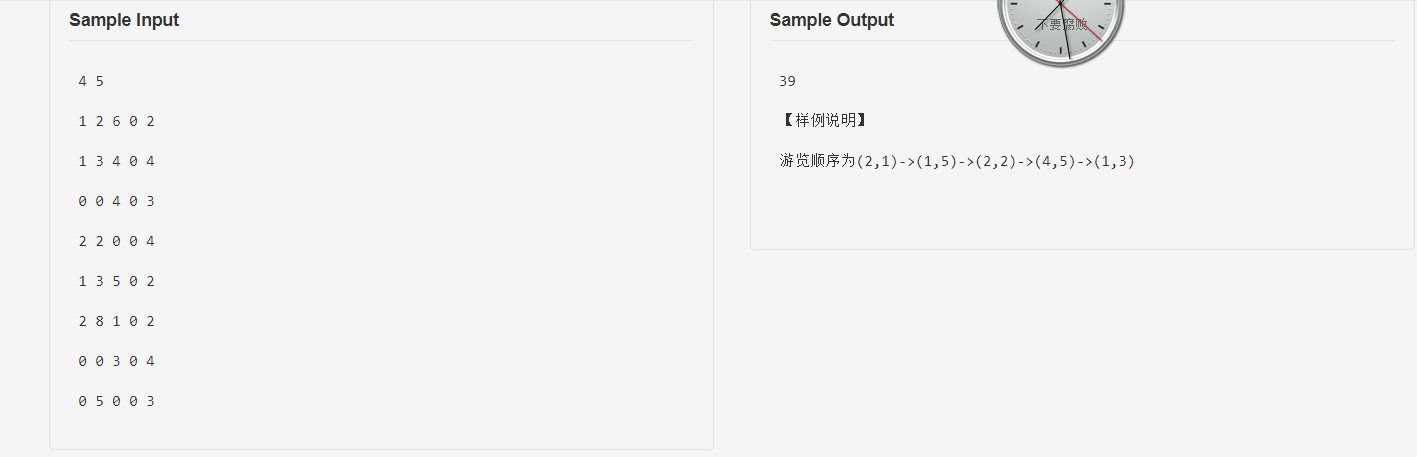
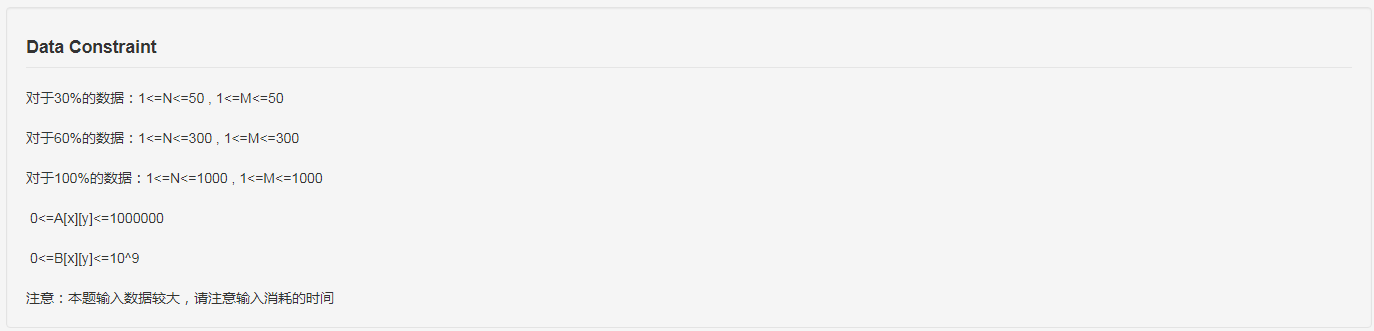
思路

这道题看上去就像一个动态规划！但是还是要把矩阵压成一行。

然后按 \(A\)数组 将结构体从小到大排个序。

随后我们开始了动规标准步骤：

确定状态

很显然， \(f_i\) 表示游览完第\(~i~\)个景点是的最长时间。

Q(动规小白为啥动规小白要做这题啊)：怎么看粗来的？？？

A：动规不是一维不行加一维的吗

确定转移方程

有了这个状态相信动规小白也能看粗来转移方程吧！

那么我们假设看完了第\(j\)个景点后就去了第\(i\)个景点(\(j~ \rightarrow ~i\))。

那么我们的方程就显而易见了。

\[\begin{matrix}f_i = max\{ f_j + (| ~ x_i - x_j ~ | + | ~ y_i-y_j ~ |) \}+B_i\\ =max\{ f_j + dis(i, j)\}+B_i~~~~~~~~~~~~~~~~~~~~\end{matrix}
\]

温馨提示：

可以发现直接暴力这么做的时间复杂度是\(O((nm)^2)\)

即使我们的题目限时两秒也会炸！！！

Q：怎么办呢？？？

卡常！！！

1、

如果\(j\)直接从\(1\)开始枚举就会有冗余的情况:

假设你的\(A_i\)是\(4\)。

\(A_{1 \sim i-1}\)分别是\(\{ 1,1,1,1,1,2,2,2,3 \}\)。

你肯定选\(3\)都要比选其他的数要强（请读者自行理解），所以从\(3\)的那里开始

2、

使用

register

SPFA

是的又是很明显地就可以看出，这题可以用最短路。

存邻接表时就只存比第\(i\)个小的就行了，剩下的就是SPFA模板了

最后

关于SPFA

• 它死了