FIFO形成3x3矩阵

　　Verilog生成矩阵一般是使用shift_ip核，但其实用两个FIFO也行。最近刚好学到这种方法，把原理总结一下。

要求

　　现在有10x5的数据和对应数据有效指示信号，数据为0~49，要用FPGA对其生成3x3矩阵，以便后面进行一些矩阵运算。

第一步，计数器行列规划

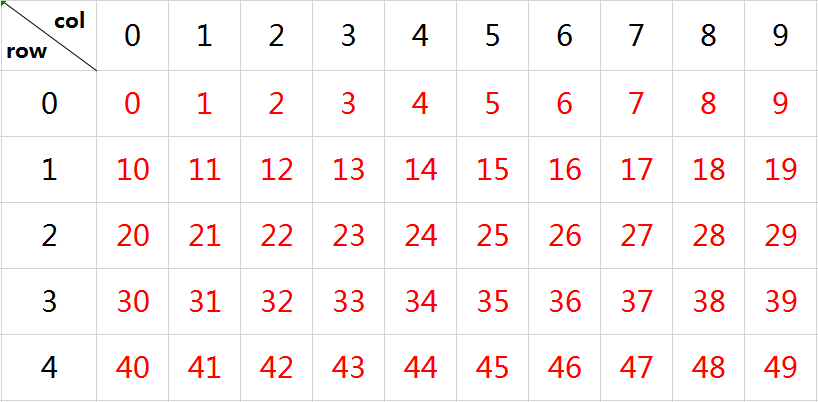
　　首先想到是计数，数据每来一个，cnt_col 就计1下，cnt_col 计满10下时再用cnt_row 计一下，cnt_row 共计5下，这样数据就变成了10x5，如下图所示:

第二步，FIFO形成三行数据

　　用两个FIFO进行将数据进行缓存。数据来的时候FIFO_1就直接写入，最后两行则不写。来第二行数据的时候FIFO_2就写入，最后一行则不写。这里的行就是用到第一步的计数了。FIFO_1和FIFO_2共用读使能，来第三行数据时就一起读，这时第三行数据来了，配合FIFO_1和FIFO_2读出来的数据，刚好形成时序对齐的3行数据。

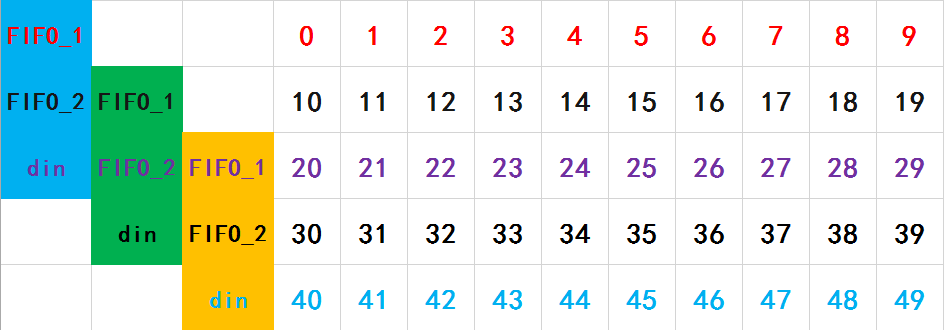
　　如果所示，上图的FIFO_1写进的是0~29，从第三行开始读出的数据也依次是0~29，读到第5行的末尾刚好读干净全部数据。FIFO_2写进的是10~39，从第三行开始读出的数据也依次是10~39，读到第5行的末尾刚好读干净全部数据。

　　即：FIFO_1写数据，最后两行数据不写进去；FIFO_2写数据，第一行数据和最后一行数据不写进去；FIFO_1和FIFO_2共用读使能，都从第三行数据刚开始时读。这时FIFO_1、FIFO_2、刚进来的din就形成了三行基本对齐的数据。这里形成了基本的对齐，可以直接进行仿真，看到不齐的地方再回来打拍是最好的方式，不断调整，最后完美对齐。例如你用的FIFO是Normal模式，那din打两拍后就是真正的完美对齐。

　　这也给我一个看代码的启示，有时候看别人代码，这里打拍那里打拍，我绞尽脑汁的想也想不明白为什么，现在才知道很多地方的打拍没有那么多为什么，就是为了对齐时序，可能本来不齐，它打拍后就齐了。实在理解不来看看波形自然明白了。

　　下面的仿真波形是形成三行数据后，每一列的三个数据进行相加，结果为dout。上面的紫色部分为输入信号，红色部分为计数信号，绿色部分为FIFO_1和FIFO_2的写相关信号，橙色部分为FIFO的读相关信号，下面的紫色部分是输出信号。可以看到din打了一拍后三行数据完美对齐：0、10、20，1、11、21......因为这里用的是Normal模式，所以最后输出时是先用rd_en打了一拍后才作为if条件输出dout，相加结果是完全正确的。仔细看波形，结合上面的示意图，发现FIFO的读写运用非常之完美，什么时候写，写多少个，什么时候读。这三个问题解决了答案就出来了。注意一下的是FIFO的深度是两行数据的个数，例如这里两行数据是20个，FIFO的深度选择比20更大的32就行了。不仅是这个10x5数据，就算是640x480这种大的像素数据也是一样的原理。

第三步，打拍形成矩阵

　　这步其实最好理解，形成矩阵只需要一起打拍就OK了。要注意的是：在什么条件下进行打拍？答案是可以是FIFO的共同读使能信号rd_en或者进来的数据有效指示信号din_vld。用rd_en打拍，则后面的运算时前两行的数据是默认丢弃的，这在图像处理上经常用到。用din_vld打拍，则前两行数据是看做补0，也是经常用到的方法。例如新进来的数据在对齐那打了一拍，变成data，FIFO_1、FIFO_2读出的数据是q_1，q_2，那么他们三个信号一起打三拍，就形成了一个对齐的矩阵了。

always @(posedge clk or negedge rst_n) begin
    if(!rst_n) begin
        {data_r3, data_r2, data_r1} <= {'b0};
        { q_2_r3,  q_2_r2,  q_2_r1} <= {'b0};
        { q_1_r3,  q_1_r2,  q_1_r1} <= {'b0};
    end
    else if(good_en)begin
        {data_r3, data_r2, data_r1} <= {data_r2, data_r1, data};
        { q_2_r3,  q_2_r2,  q_2_r1} <= { q_2_r2,  q_2_r1, q_2 };
        { q_1_r3,  q_1_r2,  q_1_r1} <= { q_1_r2,  q_1_r1, q_1 };
    end
end

　　具体的代码就不贴了，原理已经说的很清楚了。学会形成矩阵对我们后续的算法处理非常的有帮助，本设计也是为了做后面的Sobel边缘检测做基础。

　　其实生成矩阵用Shift_ip核更简单，下次再总结吧！

参考资料：[1] 威三学院FPGA教程

　　　　   [2] NingHeChuan.FPGA计算3行同列数据之和