简单地判断判断两矩形相交/重叠 C#

最近需要用到矩形相交算法的简单应用，所以特地拿一个很简单的算法出来供新手参考，为什么说是给新手的参考呢因为这个算法效率并不是很高，但是这个算法只有简简单单的三行。程序使用了两种方法来判断是否重叠/相交，如果有兴趣可以看一下，如果觉得有bug可以留言。代码仅供参考。

C#中矩形的方法为Rectangl(起始点坐标, 矩形的大小)或Rectangl(起始点x坐标, 起始点y坐标, 矩形宽, 矩形高)，起始点为矩形区域的左上角。

方法一

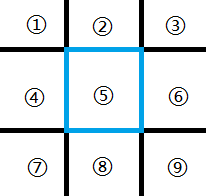
姑且叫做“井字法”吧，延长其中一个矩形的四边使其形成一“井”字（如图）并划分成九块区域，分区域来判断另一个矩形的点是否在此矩形内。

1.当生成的矩形的起始坐标点在3，6，7，8，9区域时，所生成的矩形必定不相交；

2.当生成的矩形起始点坐标在1，2，4区域时候，保证新矩形的右下角点的x坐标小于待比较矩形起始点的x坐标 或  新矩形的右下角点的y坐标小于待比较矩形起始点的y坐标 即可；

3.当生成的矩形位于5区域内时，只要保证新矩形右下角点的x和y坐标小于待比较矩形右下角点的x和y坐标即可；

4.在考虑两矩形是否重叠时不需要考虑第3条，当需要考虑是否内含时需要用第3条判断。

参考代码：

             int flag = ; //设置标记值，默认为重叠
             if (rectangle1.X > rectangle2.X + rectangle2.Width || rectangle1.Y > rectangle2.Y + rectangle2.Height) flag++; //初始点在3，6，7，8，9区域
             else if (rectangle1.X + rectangle1.Width < rectangle2.X || rectangle1.Y + rectangle1.Height < rectangle2.Y) flag++; //初始点在1区域
             else if (rectangle1.X > rectangle2.X && rectangle1.Y > rectangle2.Y && rectangle1.X + rectangle1.Width < rectangle2.X + rectangle2.Width && rectangle1.Y + rectangle1.Height < rectangle2.Y + rectangle2.Height) flag++; //初始点在5区域

             if (flag == ) textBox1.Text = "重叠";
             else textBox1.Text = "不重叠";

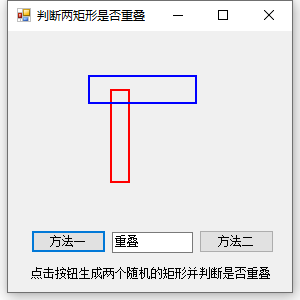
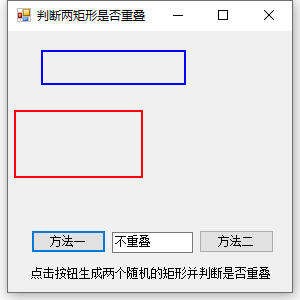
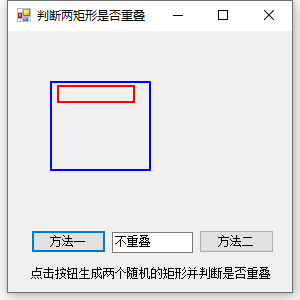
结果演示：

方法二

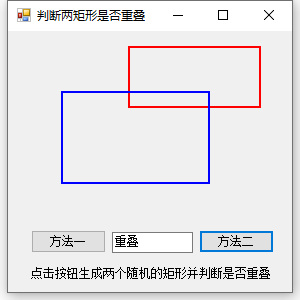
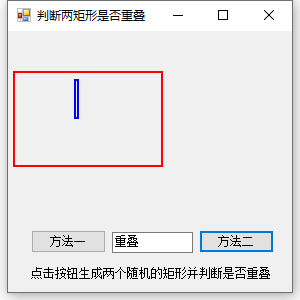
这个就简单多了，直接使用IntersectsWith方法直接可以判断是否重叠，是不是简单多了？但是它只能判断两个矩形是否重叠，内含的情况也算在重叠之内，需要使用此方法时可以考虑方法一。

 if (rectangle1.IntersectsWith(rectangle2)) textBox1.Text = "重叠";
             else textBox1.Text = "不重叠";

结果演示：

 

后记

此代码没有详细考虑边界相切问题，需要需要读者再加以考虑修改，也仅仅是提供新手一些思路或来考虑更复杂的推广应用，同时附源代码于文末供参考。另外时间、水平有限，代码难免有些小问题望读者海涵。

源代码：https://files-cdn.cnblogs.com/files/shenyuanfeng/RectangleIntersect.zip