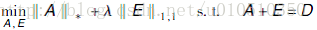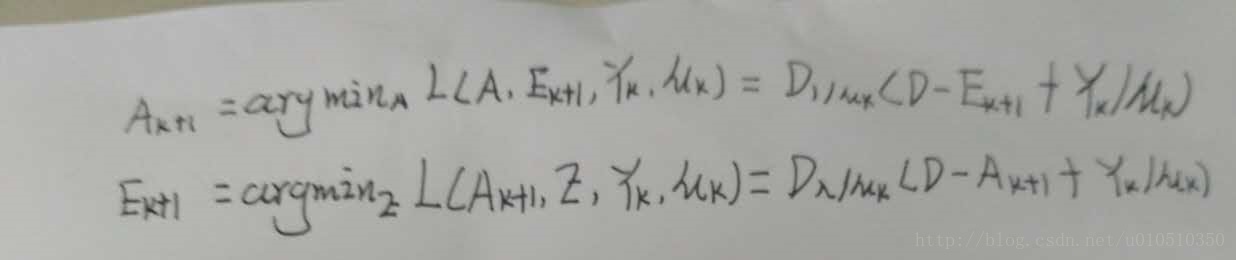Rubost PCA 优化
Rubost PCA 优化
最近一直在看Robust PCA做背景建模的paper, 顺便总结了一下了Robust PCA.前面一篇博客介绍了PCA与Robust PCA区别,本篇博客总结Robust PCA 常见的优化方法,欢迎交流学习。在这里强烈推荐一篇博客Rachel Zhang的Robust PCA 学习笔记。
1.预备知识
2.问题描述
许多实际应用中已知的数据矩阵D往往是低秩或近似低秩的,但存在随机幅值任意大且分布稀疏的误差破坏了原有数据的低秩性,为了恢复矩阵D的低秩结构,可将矩阵D分解为两个矩阵之和,即D=A+E,其中矩阵A和E未知,但A是低秩的,E是稀疏的。 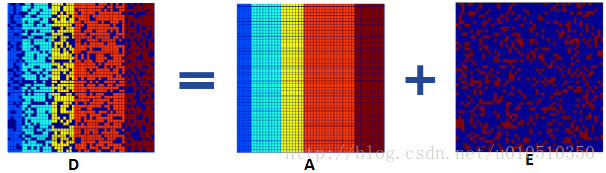
当矩阵E的元素服从独立同分布的高斯分布时,可用经典的PCA来获得最优的矩阵A,即转换为如下最优化问题: 
当E为稀疏的大噪声矩阵时,同时引入折中因此,此问题可转化为如下优化问题: 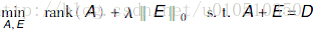
上式中秩函数、0范数均非凸,变成了NP-hard问题,需要对其松弛,方可进行优化。由范数知识可知,核范数是秩函数的凸包,1范数是0范数的凸包,所以上述NP-hard问题松弛后可转化凸优化问题:
3.Rubost PCA优化
增广拉格郎日乘子法(Augmented Lagrang Multipliers)
交替方向法(Alternating Direction Methods)
ADM 是对ALM的改善,加快了收敛速度,又称为不精确拉格朗日乘子法。
迭代阈值法(Iterative Thresholding)
**加速近端梯度(Accelerated Proximal Gradient)
**
将优化问题式的等式约束松弛到目标函数中,得到如下的拉格朗日函数:
f(A,E)的Frechet梯度Lipschitz连续性推导 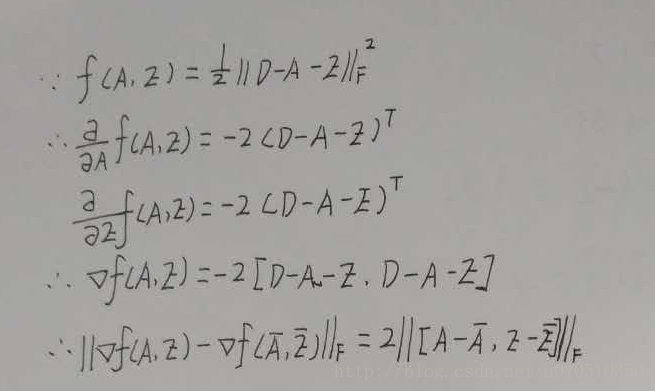
f(x)二次逼近推导
4.Rubost PCA优化总结
IT算法的迭代形式简单且收敛,但收敛速度比较慢,且很难选取合适的步长;APG与IT算法类似,但它却大大降低了迭代次数;ALM比APG快很多,而且ALM可以达到较高的精度,需要较低的存储空间。不精确拉格朗日乘子法(IALM)改善了EALM,不需要求解精确解,速度较快。
参考
1. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices
2. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix
3. A Singular Value Thresholding Algorithm for Matrix Completion
4. Sparse and Low-Rank Matrix Decomposition via Alternating Direction Methods
5. Robust Principal Component Analysis
6. http://blog.csdn.net/tiandijun/article/details/44917237
Rubost PCA 优化的更多相关文章
- 机器学习公开课笔记(8):k-means聚类和PCA降维
K-Means算法 非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括: 市场划分(Market Segmentation) 社交网络分析(Social Network Analysis ...
- Andrew Ng机器学习课程笔记--week8(K-means&PCA)
Unsupervised Learning 本周我们讲学习非监督学习算法,会学习到如下概念 聚类(clustering) PCA(Principal Componets Analysis主成分分析), ...
- 主成分分析(PCA)原理总结
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一.在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用.一般我们提到降维最容易想到的算法就 ...
- 数据降维技术(1)—PCA的数据原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- 主成分分析 (PCA) 与其高维度下python实现(简单人脸识别)
Introduction 主成分分析(Principal Components Analysis)是一种对特征进行降维的方法.由于观测指标间存在相关性,将导致信息的重叠与低效,我们倾向于用少量的.尽可 ...
- 机器学习笔记----四大降维方法之PCA(内带python及matlab实现)
大家看了之后,可以点一波关注或者推荐一下,以后我也会尽心尽力地写出好的文章和大家分享. 本文先导:在我们平时看NBA的时候,可能我们只关心球员是否能把球打进,而不太关心这个球的颜色,品牌,只要有3D效 ...
- PCA原理与实践
在对数据进行预处理时,我们经常会遇到数据的维数非常之大,如果不进行相应的特征处理,那么算法的资源开销会很大,这在很多场景下是我们不能接受的.而对于数据的若干维度之间往往会存在较大的相关性,如果能将数据 ...
- PRML读书会第十二章 Continuous Latent Variables(PCA,Principal Component Analysis,PPCA,核PCA,Autoencoder,非线性流形)
主讲人 戴玮 (新浪微博: @戴玮_CASIA) Wilbur_中博(1954123) 20:00:49 我今天讲PRML的第十二章,连续隐变量.既然有连续隐变量,一定也有离散隐变量,那么离散隐变量是 ...
- PCA算法是怎么跟协方差矩阵/特征值/特征向量勾搭起来的?
PCA, Principle Component Analysis, 主成份分析, 是使用最广泛的降维算法. ...... (关于PCA的算法步骤和应用场景随便一搜就能找到了, 所以这里就不说了. ) ...
随机推荐
- Java逻辑分页代码
前台jsp代码如下: <%@ page language="java" contentType="text/html; charset=UTF-8" pa ...
- Java开发手册-编程规约精选
# Java开发手册-编程规约精选 ## 总约 - 采用驼峰写法 ## 变量 - 首字母小写 ## 方法 - 方法名首字母小写- 参数首字母小写 ## 引用 - <阿里巴巴Java开发手册> ...
- CSS清除浮动方法集合
CSS清除浮动方法集合 一.浮动产生原因 - TOP 一般浮动是什么情况呢?一般是一个盒子里使用了CSS float浮动属性,导致父级对象盒子不能被撑开,这样CSS float浮动就产生了. ...
- Windows下通过命令行 获取文件详细信息
@echo off echo version: wmic datafile where Name="C:\\Product\\File\\Release\\1.1.1\\File.exe&q ...
- openresty开发系列15--lua基础语法4表table和运算符
openresty开发系列15--lua基础语法4表table和运算符 lua中的表table 一)table (表)Table 类型实现了一种抽象的"关联数组".即可用作数组,也 ...
- ISO/IEC 9899:2011 条款6.9.1——函数定义
6.9.1 函数定义 语法 1.function-definition: declaration-specifiers declarator declaration-listopt ...
- 算法习题---5.1大理石在哪(UVa10474)
一:题目 现有N个大理石,每个大理石上写了一个非负整数.首先把各数从小到大排序,然后回答Q个问题.每个问题问是否有一个大理石写着某个整数x,如果是,还要回答哪个大理石上写着x.排序后的大理石从左到右编 ...
- php cURL error 60: SSL certificate problem: unable to get local issuer certificate 解决办法
错误例子如下: php5.6以上的版本会出现这种问题 关于“SSL证书问题:无法获取本地颁发者证书”错误.很明显,这适用于发送CURL请求的系统(并且没有服务器接收请求) 1)从https://cur ...
- Java编程实战宝典PDF (中文版带书签)
Java编程实战宝典PDF 目录 第1篇 Java基础知识入门第1章 Java的开发运行环境( 教学视频:57分钟)1.1 Java运行原理与Java虚拟机1.1.1 Java运行原理简述1.1.2 ...
- linux用户解锁
pam_tally2 --user=username #查看 pam_tally2 --user=username --reset #重置