动态规划-多维DP

1.最大正方形

我的瞎猜分析：

　　　　

　　

　　

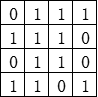
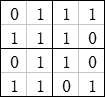
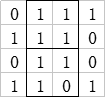
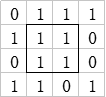
我的瞎猜算法：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>

#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 101
#define MAX 1<<30
#define V vector<int>

using namespace std;

int dp[LEN][LEN][LEN];
int a[LEN][LEN];

int main(){
    freopen("D:/CbWorkspace/动态规划/最大正方形.txt","r",stdin);
    int n,m,i,j,v,k;
    I("%d%d",&n,&m);
    F(i,,n+) F(j,,m+) {
        I("%d",&a[i][j]);
        if(a[i][j]) dp[i][j][]=;
    }
    int ans=;
    for(v=;v<n;v++){
        for(i=;i+v<=n;i++){
            for(j=;j+v<=m;j++){
                dp[i][j][v+]=dp[i][j][v];
                if(dp[i][j][v]==v){
                    bool flag=;
                    for(k=j;k<=j+v;k++){            //横向侧边
                        if(!a[i+v][k]){
                            flag=;
                            break;
                        }
                    }
                    if(flag) for(k=i;k<i+v;k++){    //纵向侧边
                        if(!a[k][j+v]){
                            flag=;
                            break;
                        }
                    }
                    if(flag){
                        dp[i][j][v+]++;
                    }
                }
                ans=max(ans,dp[i][j][v+]);
            }
        }
    }
    printf("%d",ans);
    return ;
}

---

我的瞎猜算法：

#include <stdio.h>
#include <memory.h>
#include <math.h>
#include <string>
#include <vector>
#include <set>
#include <stack>
#include <queue>
#include <algorithm>
#include <map>

#define I scanf
#define OL puts
#define O printf
#define F(a,b,c) for(a=b;a<c;a++)
#define FF(a,b) for(a=0;a<b;a++)
#define FG(a,b) for(a=b-1;a>=0;a--)
#define LEN 101
#define MAX 1<<30
#define V vector<int>

using namespace std;

int dp[LEN][LEN][LEN];
int a[LEN][LEN];

int main(){
    freopen("D:/CbWorkspace/动态规划/最大正方形.txt","r",stdin);
    int n,m,i,j,v,k;
    I("%d%d",&n,&m);
    F(i,,n+) F(j,,m+) {
        I("%d",&a[i][j]);
        if(a[i][j]) dp[i][j][]=;
    }
    int ans=;
    for(v=;v<n;v++){
        for(i=;i+v<=n;i++){
            for(j=;j+v<=m;j++){
                dp[i][j][v+]=dp[i][j][v];
                if(dp[i][j][v]==v){
                    bool flag=;
                    for(k=j;k<=j+v;k++){            //横向侧边
                        if(!a[i+v][k]){
                            flag=;
                            break;
                        }
                    }
                    if(flag) for(k=i;k<i+v;k++){    //纵向侧边
                        if(!a[k][j+v]){
                            flag=;
                            break;
                        }
                    }
                    if(flag){
                        dp[i][j][v+]++;
                    }
                }
                ans=max(ans,dp[i][j][v+]);
            }
        }
    }
    printf("%d",ans);
    return ;
}