NOJ——1642简单的图论问题?（BFS+优先队列）

• [1642] 简单的图论问题?

• 时间限制: 5000 ms　内存限制: 65535 K
• 问题描述

• 给一个 n 行 m 列的迷宫,每个格子要么是障碍物要么是空地。每个空地里都有一个权值。你的
  任务是从找一条(r1,c1)到(r2,c2)的路径,使得经过的空地的权值之和最小。每一步可以往上下
  左右四个方向之一移动一格,但不能斜着移动,也不能移动到迷宫外面或者进入障碍物格子。

  如下图,灰色格子代表障碍物。路径 A->B->D->F->E 的权值为 10+3+6+14+8=41,它是从 A 到 E 的最优路径。注意,如果同一个格子被经过两次,则权值也要加两次。

  

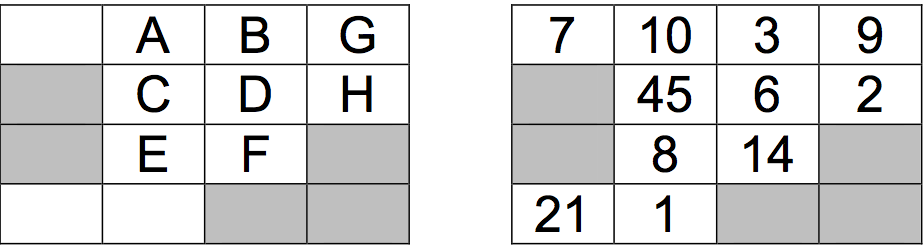
  为了让题目更有趣(顺便增加一下难度),你还需要回答另外一个问题:如果你每次必须转弯 (左转、右转或者后退,只要不是沿着上次的方向继续走即可),最小权值是多少?比如,在
  上图中,如果你刚刚从 A 走到 B,那么下一步你可以走到 D 或者 A,但不能走到 G。在上图
  中,A 到 E 的最优路径是 A->B->D->H->D->F->E,权和为 10+3+6+2+6+14+8=49。注意,D 经
  过了两次。

• 输入
• 输入包含不超过 10 组数据。每组数据第一行包含 6 个整数 n, m, r1, c1, r2, c2 (2<=n,m<=500, 1<=r1,r2<=n, 1<=c1,c2<=m). 接下来的 n 行每行包含 m 个格子的描述。每个格子要么是一个 1~100 的整数,要么是星号"*"(表示障碍物)。起点和终点保证不是障碍物。
• 输出
• 对于每组数据,输出两个整数。第一个整数是“正常问题”的答案,第二个整数是“有趣问 题”的答案。如果每个问题的答案是“无解”,对应的答案应输出-1。
• 样例输入

• 4 4 1 2 3 2
  7 10 3 9

  * 45 6 2

  * 8 14 *
  
21 1 * *
  2 4 1 1 1 4
  1 2 3 4
  9 * * 9
  2 4 1 1 1 4
  1 * 3 4
  9 9 * 9 

• 样例输出

• Case 1: 41 49
  Case 2: 10 -1
  Case 3: -1 -1

• 提示

• 无

• 来源

• 第十一届“蓝狐网络杯”湖南省大学生计算机程序设计竞赛

这题让我知道了其实BFS也是可以计算权值不同的最短路的。而且给出一般矩阵图的情况下比肯定比SPFA好用。学习到了第一个答案比较简单，第二个就用三维的数组visd来记录这个点是否被某个方向来的now给访问过，来过滤掉绕圈圈的情况，因此就不能在用vis了因为转弯是可以走原路的

代码：

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<sstream>
#include<cstring>
#include<cstdio>
#include<string>
#include<deque>
#include<stack>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
#define INF 0x3f3f3f3f
#define MM(x) memset(x,0,sizeof(x))
#define MMINF(x) memset(x,INF,sizeof(x))
typedef long long LL;
const double PI=acos(-1.0);
const int N=505;
struct info
{
	int w;
	int x,y;
	int pre;
	bool operator<(const info &b)const
	{
		return w>b.w;
	}
};
inline info operator+(const info &a,const info &b)
{
	info c;
	c.x=a.x+b.x;
	c.y=a.y+b.y;
	return c;
}
info S,T;
info direct[4]={{0,1,0,0},{0,-1,0,0},{0,0,1,0},{0,0,-1,0}};
int n,m;
int pos[N][N];
int vis[N][N];
int visd[N][N][4];
priority_queue<info>Q;
void init()
{
	MM(pos);
	MM(vis);
	while (!Q.empty())
		Q.pop();
}
bool check(const info &a)
{
	if(a.x>=0&&a.x<n&&a.y>=0&&a.y<m&&!vis[a.x][a.y]&&pos[a.x][a.y])
		return true;
	return false;
}
int main(void)
{
	int i,j,tcase=0;
	char s[5];
	while (~scanf("%d%d%d%d%d%d",&n,&m,&S.x,&S.y,&T.x,&T.y))
	{
		init();
		for (i=0; i<n; i++)
		{
			for(j=0; j<m; j++)
			{
				scanf("%s",s);
				if(s[0]=='*')
					pos[i][j]=0;
				else
					sscanf(s,"%d",&pos[i][j]);
			}
		}
		--S.x;--S.y;--T.x;--T.y;
		S.w=pos[S.x][S.y];
		Q.push(S);
		vis[S.x][S.y]=1;
		int ans1=-1,ans2=-1;
		while (!Q.empty())
		{
			info now=Q.top();
			Q.pop();
			if(now.x==T.x&&now.y==T.y)
			{
				ans1=now.w;
				break;
			}
			for (i=0; i<4; i++)
			{
				info v=now+direct[i];
				v.w=now.w+pos[v.x][v.y];
				if(check(v))
				{
					vis[v.x][v.y]=1;
					Q.push(v);
				}
			}
		}
		MM(vis);MM(visd);
		while (!Q.empty())
			Q.pop();
		S.pre=-1;
		vis[S.x][S.y]=1;
		Q.push(S);
		while (!Q.empty())
		{
			info now=Q.top();
			Q.pop();
			if(now.x==T.x&&now.y==T.y)
			{
				ans2=now.w;
				break;
			}
			for (i=0; i<4; i++)
			{
				info v=now+direct[i];
				v.w=now.w+pos[v.x][v.y];
				v.pre=i;
				if(check(v)&&v.pre!=now.pre&&(!visd[v.x][v.y][v.pre]))
				{
					visd[v.x][v.y][v.pre]=1;
					Q.push(v);
				}
			}
		}
		printf("Case %d: %d %d\n",++tcase,ans1,ans2);
	}
	return 0;
}