旋转矩阵 The Rotation Matrix

参考：

http://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/geometry/how-does-matrix-work-part-1

http://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/geometry/how-does-matrix-work-part-2

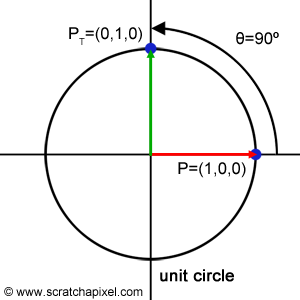
在scratchapixel的教程中，旋转矩阵是一种能将点或者向量绕某个轴旋转的矩阵，这里说的点和向量，是以自然基（或称为标准基）为基底的。

如上图，Z轴为贯穿屏幕的轴，点P绕Z轴逆时针旋转到P_t，记旋转矩阵为R，则三者的关系是：P • R = P_t

在scratchapixe的l教程中，作者最后试算出了这样的R，但并未做证明，这样的R，由旋转的轴不同，分别有绕X轴旋转的R_x，绕Y轴旋转的R_y，绕Z轴旋转的R_z：

其中Θ是逆时针旋转的角度

假设点P的坐标是(1,0,0)，让它绕Z轴顺时针旋转Θ角（弧度单位），那么P_t的坐标是(cos(Θ), sin(Θ), 0)，例如Θ是π/2时，P_t的坐标是(0, -1, 0)

假设点P的坐标是(0,1,0)，让它绕Z轴顺时针旋转Θ角（弧度单位），那么P_t的坐标是(-sin(Θ), cos(Θ), 0)，例如Θ是π/2时，P_t的坐标是(1, 0, 0)

刚好是分别是R_z的前两行，在scratchapixe的l教程中说，“理解矩阵R_z的关键一点，就是其每一行代表了坐标系中的一个轴，整个R_z代表了一组基”

这其实有点难以理解，于是翻出居余马的线性代数，第四章讲向量空间与线性变换，里面有关于基的定义是这样的：

定义：设有序向量组B={ß₁, ß_2…ß_n}是实向量空间Rⁿ的子集，如果B线性无关，则Rⁿ中任一向量α，均可由B线性表示即

　　α = a₁ß₁ + a₂ß₂ + … + a_nß_n

就称B是Rⁿ这个实向量空间中的一组基（或基底），有序数组(a₁, a₂ … a_n)是向量α关于基B（或说在基B下）的坐标，记作α_B = (a₁, a₂ … a_n) 或 α_B = (a₁, a₂ … a_n) ^T

可以看到，scratchapixe阐述的角度是如何让一个点或者向量，乘以一个矩阵，移动到同一个坐标系的另外一个位置

而线性代数上，阐述的是同一个点在两组不同的基的坐标，以及两组基之间的过度矩阵怎样计算

而二者的内在联系具体怎样理解，我还要继续学习一下