PM的正交解调法
1.PM的模拟调制过程
PM信号是一种相位调制信号,其携带的信息保存在其信号的相位中,通过改变载波的相位来实现基带数据的传输。
其函数表达式如下:
\]
其中:
\(A\):表示载波幅度。
\(m(t)\):表示基带信号。
\(w_c\):表示载波信号角度增量。
\(K_f\):是调制灵敏度。
正交调制法公式如下:
Q(t) = sin(K_f*m(t)) \\
s(t) = A*(I(t)*cos(w_c*t) - Q(t)*sin(w_c*t))
\]
2.PM的数字正交解调
原理:
对于I路,其中\(\varphi\)表示调制载波与解调载波的相位差:
I(n) & = LPF(s(n)*cos(w_c*n + \varphi)) \\
& = \frac{cos(K_f*m(n))*cos(\varphi) + sin(K_f*m(n))*sin(\varphi)}{2} \\
& = \frac{1}{2}*cos(K_f*m(n) - \varphi)
\end{array}
\]
对于Q路:
Q(n) & = LPF(s(n)*sin(w_c*n + \varphi)) \\
& = \frac{cos(K_f*m(n))*sin(\varphi) - sin(K_f*m(n))*cos(\varphi)}{2} \\
& = \frac{1}{2}*sin(K_f*m(n) - \varphi)
\end{array}
\]
同时:
&\ \frac{Q(n)}{I(n)} = \frac{sin(K_f* m(n)- \varphi)}{cos(K_f* m(n)- \varphi)} = tan(K_f* m(n) - \varphi) \\
&\ M(n) = arctan(\frac{Q(n)}{I(n)}) = K_f* m(n) - \varphi\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
(\frac{Q(n)}{I(n)}) \in (-\pi/2\space\space\space\space\pi/2)
\end{array}
\]
注:上式推算中使用了arctan函数,其中arctan的输入范围\((-\pi/2\space\space\space\space\pi/2)\)。当范围超过将计算错误。所以将使用MATLAB的atan2函数进行计算。
\]
3.MATLAB仿真
仿真代码:
fs = 20000;%采样率
l = 1E3;%基带信号点数
f = 100;%基带信号
f_c = 500;%载波信号
t = 0:1/fs:(l-1)/fs;
mt = cos(2*pi*f*t);
kf = 2;
fi = pi/3;
%% IQ信号
I = cos(kf*mt + fi);
Q = sin(kf*mt + fi);
%% 调制数据
mod_data = I.*cos(2*pi*f_c*t) - Q.*sin(2*pi*f_c*t);
%% 解调
demod = atan2(Q,I);
for i = 2:1:length(demod)
if(demod(i) >= pi)
demod(i) = demod(i) - pi*2;
elseif(demod(i) <= -pi)
demod(i) = demod(i) + pi*2;
else
demod(i) = demod(i);
end
end
%% 去直流
dc_signal = sum(demod)/l;
demod0 = demod-dc_signal;
%% 保存IQ数据FPGA使用仿真
fid = fopen('PM.txt','w');
for i = 1:l
fprintf(fid,'%d %d\n',floor(I(i)* (2^13)),floor(Q(i)* (2^13)));
end
fclose(fid);
%% 绘制
figure
time = 4;
subplot(time,1,1);
plot(mt);
title('基带数据');
subplot(time,1,2);
plot(mod_data);
title('调制数据');
subplot(time,1,3);
plot(demod);
title('解调数据');
subplot(time,1,4);
plot(demod0);
title('解调数据(去直流)');
结果:
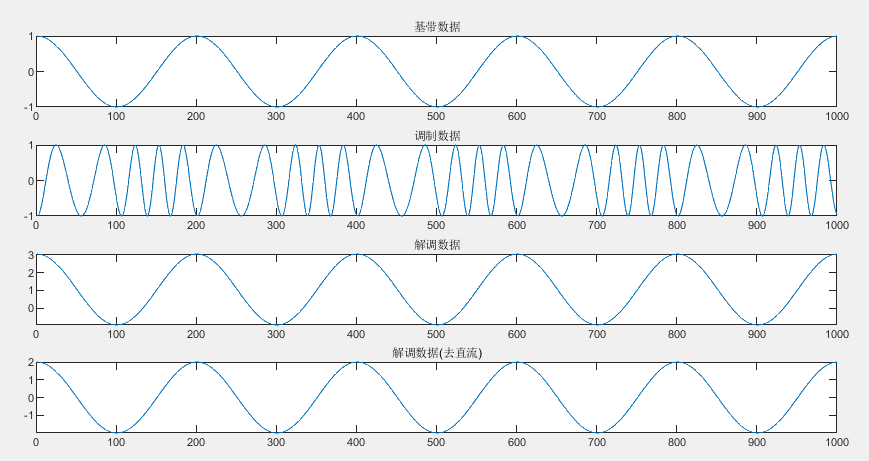
4.FPGA解调
逻辑代码:
module pm_demod(
input clk ,
input rst ,
//解调参数
input i_valid ,
input [15:0] i_data_i ,
input [15:0] i_data_q ,
output o_rdy ,
output [15:0] o_data
);
wire pm_valid ;
wire [23:0] pm_i ;
wire [23:0] pm_q ;
wire pm_rdy ;
wire [47 : 0] m_axis_dout_tdata ;
//AM 解调
assign pm_valid = i_valid ;
assign pm_i = {{8{i_data_i[15]}},i_data_i} ;
assign pm_q = {{8{i_data_q[15]}},i_data_q} ;
cordic_translate cordic_translate (
.aclk (clk ), // input wire aclk
.s_axis_cartesian_tvalid (pm_valid ), // input wire s_axis_cartesian_tvalid
.s_axis_cartesian_tdata ({pm_i,pm_q} ), // input wire [47 : 0] s_axis_cartesian_tdata
.m_axis_dout_tvalid (pm_rdy ), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata (m_axis_dout_tdata ) // output wire [47 : 0] m_axis_dout_tdata
);
assign o_data = m_axis_dout_tdata[24 +:16];
assign o_rdy = pm_rdy;
endmodule
仿真代码:
module tb_pm_demod();
reg clk;
reg rst;
initial begin
clk <= 0;
rst <= 1;
#300
rst <= 0;
end
always #(100/2) clk <=~clk;
reg valid;
reg [15:0] din_i;
reg [15:0] din_q;
wire o_rdy ;
wire [15:0] o_data ;
pm_demod pm_demod(
.clk (clk),
.rst (rst),
.i_valid (valid),
.i_data_i (din_i),
.i_data_q (din_q),
.o_rdy (o_rdy ),
.o_data (o_data )
);
integer file_rd; //定义数据读指针
integer flag;
initial begin //打开读取和写入的文件,这里的路径要对
file_rd = $fopen("PM.txt","r");
end
reg [15:0] cnt;
always @(posedge clk)begin
if(rst)begin
din_i <= 0;
din_q <= 0;
cnt <= 0;
valid <= 0;
end
else if(cnt <= 1000)begin
valid <= 1;
flag = $fscanf(file_rd,"%d %d",din_i,din_q);
cnt <= cnt + 1;
end
else begin
$fclose(file_rd);
$stop();
end
end
endmodule
仿真结果:
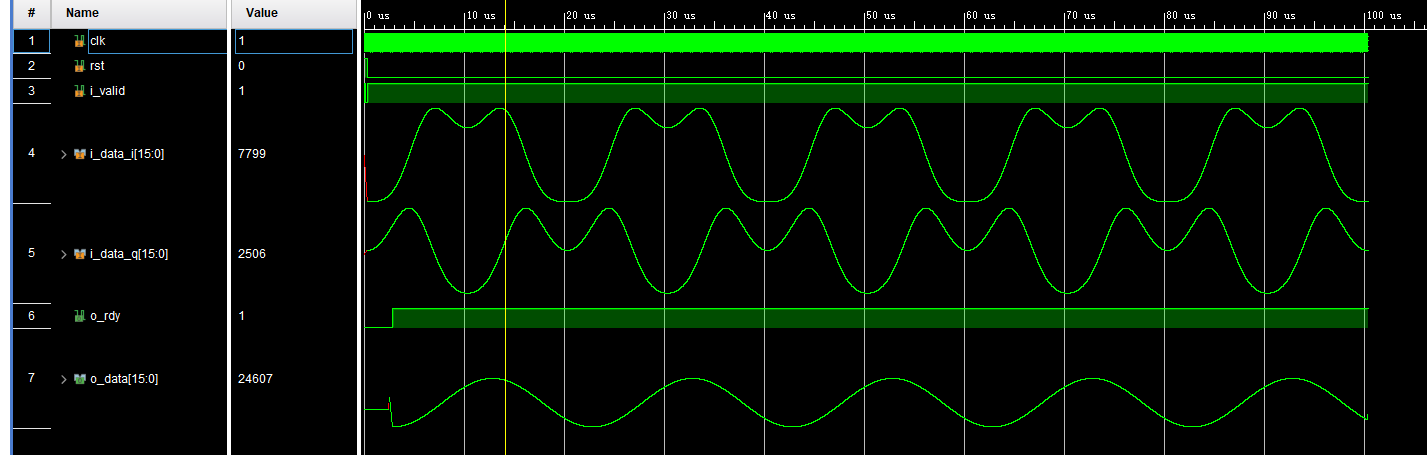
PM的正交解调法的更多相关文章
- Python实现正交实验法自动设计测试用例
1.简介 正交试验法是研究多因素.多水平的一种试验法,它是利用正交表来对试验进行设计,通过少数的试验替代全面试验,根据正交表的正交性从全面试验中挑选适量的.有代表性的点进行试验,这些有代表性的点具备了 ...
- 正交实验法之 Allpairs电商项目用例设计实战
一.正交实验法概述 正交实验法是研究多因素多水平的一种方法,它是通过正交表挑选部分有代表性的水平组合试验替代全面试验.这些有代表性的组合试验具备了"均匀分散,整齐可比"的特点.正交 ...
- AGC电路以及AD8347正交解调芯片
1.AGC电路的工作原理 1.1AGC电路的用途 随着电磁环境的日益恶化, 不同频段电磁信号之间的相互串扰, 以及可能出现的人为干扰, 将会导致接收机输入端口的信号动态范围较大, 一旦出现电路饱和或是 ...
- 浅谈压缩感知(九):正交匹配追踪算法OMP
主要内容: OMP算法介绍 OMP的MATLAB实现 OMP中的数学知识 一.OMP算法介绍 来源:http://blog.csdn.net/scucj/article/details/7467955 ...
- 方差分析3——正交表与正交实验设计(R语言)
正交试验设计(orthogonal design简称正交设计(orthoplan),是利用正交表(orthogonal table)科学地安排与分析多因素试验的方法,是最常用的试验设计之一.正交表是一 ...
- gardner 算法matlab实现
% 仿真4比特原始数据与星座图的编码映射过程: % 完成16QAM信号的调制解调: % 基带信号符号速率 ps =1Mbps: % 成形滤波器的滚降因子 a=0.8: % 载波信号频率fc=2MHz ...
- NCO
NCO 摘自百度百科 (数字振荡器) 锁定 本词条由“科普中国”百科科学词条编写与应用工作项目 审核 . 数字控制振荡器(NCO,numerically controlled oscillator)是 ...
- PostMan接口测试(很全面的接口测试教程)
一:理论部分 1. 前言 在前后端分离开发时,后端工作人员完成系统接口开发后,需要与前端人员对接,测试调试接口,验证接口的正确性可用性.而这要求前端开发进度和后端进度保持基本一致,任何一方的进度跟不上 ...
- 移动端APP自动化测试超全基础汇总
目录 一.面试过程 1.自动化岗位要求 2.面试流程,面试类型 3.沟通技巧,不同级别要求 二.真实面试案例 1.一个输入框的面试题(有人拿到高级岗位,有人连初级都没拿到,为什么) 三.自我分析 1. ...
- Testing - 测试基础 - 用例
测试用例 是指对一项特定的软件产品进行测试任务的描述,体现测试方案.方法.技术和策略. 内容包括测试目标.测试环境.输入数据.测试步骤.预期结果.测试脚本等,并形成文档. 每个具体测试用例都将包括下列 ...
随机推荐
- 《TensorFlow+Keras自然语言处理实战》已出版
<TensorFlow+Keras自然语言处理实战>已出版 当当京东天猫均有出售.清华社官网信息如下: http://www.tup.tsinghua.edu.cn/booksCenter ...
- Android UsbDeviceManager 代码分析
USBDeviceManager是一个Android系统中用于管理USB设备的类,它是系统服务之一.其主要功能是控制USB设备的连接和断开,以及管理USB设备的权限和状态.下面是对USBDeviceM ...
- 权限控制 vue3
- Oracle ASM 常用巡检脚本
1.查看磁盘组 sqlplus "/ as sysasm" set line 200 set pagesize 200 select group_number,name,state ...
- [rCore学习笔记 031] SV39多级页表的硬件机制
看到这个题目就知道上一节提到的RISC-V手册的10.6节又有用武之地了. 这里只需注意,RV32 的分页方案Sv32支持4GiB的虚址空间,RV64 支持多种分页方案,但我们只介绍最受欢迎的一种,S ...
- springBoot项目启动卡在Root WebApplicationContext: initialization completed... (非DEBUG断点问题)
通过源码启动排查发现,初始化连接池时创建了200次,通过配置文件中将initialSize值改为10,启动时间从1分钟变为了3秒.
- 3-3 C++ vector类型
目录 3.3.0 模板(Template) vector说明 模板简介 3.3.1 vector的定义和初始化 初始化的方式 总结初始化 3.3.2 往vector中添加元素 3.3.3 vector ...
- isObjectLike:检查 value 是否是 类对象。 如果一个值是类对象,那么它不应该是 null,而且 typeof 后的结果是 "object"
function isObjectLike(value) { return value != null && typeof value == 'object';}
- C#/.NET/.NET Core技术前沿周刊 | 第 13 期(2024年11.11-11.17)
前言 C#/.NET/.NET Core技术前沿周刊,你的每周技术指南针!记录.追踪C#/.NET/.NET Core领域.生态的每周最新.最实用.最有价值的技术文章.社区动态.优质项目和学习资源等. ...
- 敏捷开发:Scrum 中的 Product Backlog 介绍
Product Backlog 产品待办列表 在计划开发产品功能时,都希望产品功能上线后,用户能够喜欢并经常使用. 因此在开发产品新功能时,就要衡量哪些产品需求是对用户最有价值,这是最应该思考的问题. ...
