2025牛客多校第六场 D.漂亮矩阵 K.最大gcd C.栈 L.最小括号串 个人题解

L.最小括号串

数组操作 #贪心

题目

思路

感谢Leratiomyces大佬赛时的提示，否则估计还一直签不了到（）

首先，贪心地构造出最优情况：数组左半部分全是(，右半部分全是)，随后通过判断给定的区间中是否包含(来决定是否调整当前序列。

对给定的区间按照左端点降序排序，这样就可以从右往左有序遍历所有区间。

设置两个指针\(id_{l},id_{r}\)：

• \(id_{l}\)指向未被调换的(中最右的(的下标
• \(id_{r}\)指向经过调换后的(中最左的(的下标

从右往左有序遍历所有区间：

• 如果当前区间右端点\(r\)在\(id_{r}\)左侧，那么说明当前区间\([l,r]\)中一定没有(，因此需要调度一个(前往\(l\)位置（尽量保证字典序小），即\(swap(ans[\ id_{l}\ ],ans[\ l\ ])\)
• 调度前需要注意\(id_{l}\)是否为0，即序列左端是否还剩余(。如果\(id_{l}==0\)而仍然需要调度(，那么必然是不合法的，输出-1

最后不要忘了遍历整个序列判断是否会存在)(的非法情况

代码实现

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<unordered_set>
#include<queue>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i++)
#define per(i, a, b) for(ll i = (a); i >= (b); i--)
#define mid ((l+r)>>1)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const int N=1e5+5;
int n,m;
struct lr{
    int l,r;
    bool operator<(const lr&t)const{
        return l>t.l;
    }
};
void solve() {
    cin>>n>>m;
    n*=2;
    vector<lr>b(m+1);
    vector<char>ans(n+1);
    rep(i,1,m){
        int l,r;cin>>l>>r;
        b[i]={l,r};
    }
    rep(i,1,n){
        if(i<=n/2)ans[i]='(';
        else ans[i]=')';
    }
    sort(b.begin()+1,b.begin()+1+m);
    int idl=n/2,idr=n+1;
    rep(i,1,m){
        int l=b[i].l,r=b[i].r;
        if(r<idr){
            if(idl<1){
                cout<<-1<<'\n';return;
            }
            swap(ans[idl],ans[l]);
            idr=l;
            idl--;
        }
    }
    int cntl=0,cntr=0;
    rep(i,1,n){
        if(ans[i]=='(')cntl++;
        else cntr++;
        if(cntr>cntl){
            cout<<-1<<'\n';return;
        }
    }
    rep(i,1,n)cout<<ans[i];
    cout<<'\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

---

C.栈

数学 #组合数 #斯特林数

题目

思路

提供一种纯数学的方法：

设\(S_{n}^m\)为长度为\(n\)的所有排列中\(size\)为\(m\)的数量

易知\(\sum_{i=1}^nS_{n}^i=n!\)，即排列数\(A_{n}^n\)

接下来可以找出他的递推：

• 当数字\(n\)不位于排列的最后一位时，\(stack\)的\(pop\)功能必定会将其\(pop\)掉，即数字\(n\)不产生贡献。数字\(n\)不位于最后一位的可能有\(n-1\)种，那么就可以将此时的情况等价于\(长度为n-1的所有排列中size为m的数量\)，即\((n-1)\times S_{n-1}^m\)
• 当数字\(n\)位于排列的最后一位时，其必然对\(size\)产生\(1\)的贡献，那么就可以将此时的情况等价于\(长度为n-1的所有排列中size为m-1的数量\)，即\(S_{n-1}^{m-1}\)
  
  综上：

\[S_{n}^m=(n-1)\times S_{n-1}^m+S_{n-1}^{m-1}
\]

则答案所求即：

\[\sum_{i=1}^n i^3·S_{n}^i
\]

为了求解答案，我们设\(sum_{j}[n]=\sum_{i=1}^ni^j·S_{n}^i\)，其中：

• \(sum_{0}[n]=\sum_{i=1}^nS_{n^i}=n!\)
• 所求答案即\(sum_{3}[n]\)

接下来我们来研究\(sum_{j}\)之间的递推：

\[\begin{align}
sum_{1}[n]&=\sum_{i=1}^ni·S_{n-1}^i\\ \\
&带入递推式S_{n}^m=(n-1)\times S_{n-1}^m+S_{n-1}^{m-1}:\\ \\
&=\sum_{i=1}^ni·[\ (n-1)S_{n-1}^i+S_{n-1}^{i-1}]\\ \\
&=(n-1)\sum_{i=1}^ni·S_{n-1}^i+\sum_{i=1}^ni·S_{n-1}^{i-1}\\ \\
&=(n-1)sum_{1}[n-1]+\sum_{i=0}^{n-1}(i+1)·S_{n-1}^i\\ \\
&=(n-1)sum_{1}[n-1]+\sum_{i=1}^{n-1}i·S_{n-1}^i+\sum_{i=1}^{n-1}S_{n-1}^i\\ \\
&=(n-1+1)sum_{1}[n-1]+sum_{0}[n-1]\\ \\
sum_{1}[n]&=n·sum_{1}[n-1]+sum_{0}[n-1]
\end{align}
\]

因此我们可以完全类比推导过程得出\(sum_{j}[n]\)的公式：

\[\begin{align}
&sum_{j}[n]=\sum_{i=1}^ni^j·S_{n}^i\\ \\
&=\sum_{i=1}^ni^j·[(n-1)S_{n-1}^i+S_{n-1}^{i-1}]\\ \\
&=(n-1)sum_{j}[n-1]+\sum_{i=1}^ni^j·S_{n-1}^{i-1}\\ \\
&=(n-1)sum_{j}[n-1]+\sum_{i=0}^{n-1}(i+1)^j·S_{n-1}^i\\ \\
&=(n-1)sum_{j}[n-1]+\sum_{i=1}^{n-1}\sum_{k=0}^jC_{j}^k·i^k·S_{n-1}^i\\ \\
&=(n-1)sum_{j}[n-1]+\sum_{k=0}^jC_{j}^k\sum_{i=1}^{n-1}i^k·S_{n-1}^i\\ \\
sum_{j}[n]&=(n-1)sum_{j}[n-1]+\sum_{k=0}^jsum_{k}[n-1]
\end{align}
\]

由此我们可以在\(o(n)\)的复杂度下递推得到\(sum_{3}[n]\)

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
const int MOD = 998244353;
const int N = 5e5 + 5;

ll ans[N], sum3[N], sum2[N], sum1[N], sum0[N];

void precompute() {
    sum0[1] = 1;sum1[1] = 1;sum2[1] = 1;sum3[1] = 1;ans[1] = 1;
    for (int n = 2; n < N; ++n) {
        sum0[n] = (n * sum0[n-1]) % MOD;
        sum1[n] = (n * sum1[n-1] + sum0[n-1]) % MOD;
        sum2[n] = (n * sum2[n-1] + 2 * sum1[n-1] + sum0[n-1]) % MOD;
        sum3[n] = (n * sum3[n-1] + 3 * sum2[n-1] + 3 * sum1[n-1] + sum0[n-1]) % MOD;
        ans[n] = sum3[n];
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    precompute();
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        cout << ans[n] << '\n';
    }
    return 0;
}

---

K. 最大gcd

数学 #gcd #差分

题目

思路

已知gcd具有特殊性质：

\[gcd(a_{1},a_{2},\dots,a_{n})=gcd(a_{1},a_{2}-a_{1},a_{3}-a_{2},\dots,a_{n}-a_{n-1})
\]

设差分数组\(b[N],b[i]=a[i]-a[i-1]\)

则对于区间\([l,r]\)内每个数都加\(k\)相当于对\(b[l]+=k,b[r+1]-=k\)

• 首先讨论整个数组都\(+k\)的情况：
  • 操作\(b[1]+=k\)即可（\(b[r+1]\)不存在）
  • 此时的gcd为\(gcd(b_{1}+k,b_{2},\dots,b_{n})\)
  • 必定存在\(k\)使得\(gcd(b_{2},b_{3},\dots,b_{n})|(b_{1}+k)\)
  • 因此该情况的gcd记为\(g_{1}=gcd(b_{2},b_{3},\dots,b_{n})\)
• 接下来讨论局部\(+k\)的情况：
  • 由于是局部操作，所以\(b_{1},b_{n}\)这两个的其中一个必定不会被\(+k\)，因此枚举\(b_{1},b_{n}\)的所有因数\(f\)
  • 若所有的\(b_{i}\)都为\(f\)的倍数，那么当前的\(f\)一定是合法的gcd
  • 若只有一个\(b_{i}\)不是\(f\)的倍数，那么一定存在一个\(k\)使得\(f|(b_{i}+k)\)，当前的\(f\)也是合法的
  • 若超过两个\(b_{i}\)不是\(f\)的倍数，那么无论怎么操作都不可能使得整个数组的gcd为\(f\)
  • 若只有两个\(b_{i}\)不是\(f\)的倍数，那么需要特殊判断。在此提供两种判断方法：
    • 方法一：
      • 设不是\(f\)的两个数为\(b_{1},b_{2}\)，则\(b_{1}=t_{1}\times f+b_{1}\%f,b_{2}=t_{2}\times f+b_{2}\%f\)
      • 令\(k=b_{1}\%f\)，则\(b_{1}-k=t_{1}\times f\)为\(f\)的倍数；
      • \(b_{2}+k=t_{2}\times f+b_{1}\%f+b_{2}\%f\)要为\(f\)的倍数，则必有\((b_{1}\%f+b_{2}\%f)\%f=0\)
      • 因此可以通过判别式\((b_{1}\%f+b_{2}\%f)\%f=0\)来确定两个\(b_{i}\)是否合法
    • 方法二：
      • 设不是\(f\)的两个数为\(b_{1},b_{2}\)且\(b_{1}-k,b_{2}+k\)为\(f\)的倍数，则有\(b_{1}\equiv k\pmod{f},b_{2}\equiv(-k)\pmod{f}\)
      • 两式相加得\((b_{1}+b_{2})\equiv0\pmod{f}\)，即\((b_{1}+b_{2})\%f=0\)
      • 因此可以通过判别式\((b_{1}+b_{2})\%f=0\)来判断两个\(b_{i}\)是否合法

特别需要注意的是，由于差分可能会导致负数，所以gcd函数返回的时候需要加绝对值

这与给传入的变量加绝对值是完全不一样的操作！

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
//#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const ll inf = 1e7 + 5;
// #define int ll
const int N=1e5+5;

ll gcd(ll a,ll b){
    if(!b)return abs(a);
    return gcd(b,a%b);
}

int a[N],b[N];
void eachT() {
    int n;cin>>n;
    bool same=1;
    int g1;
    rep(i,1,n){
        cin>>a[i],b[i]=(a[i]-a[i-1]);
        if(i==2)g1=b[2];
        if(i>=3)g1=gcd(g1,(b[i]));
        if(i>=2&&a[i]!=a[i-1])same=0;
    }
    if(same){
        cout<<0<<'\n';return;
    }
    if(n==2){
        cout<<max(a[1],a[2])<<'\n';return;
    }
    set<int>fac;
    for(int i=1;i*i<=a[1];i++){
        if(a[1]%i==0)fac.insert(i),fac.insert(a[1]/i);
    }
    for(int i=1;i*i<=a[n];i++){
        if(a[n]%i==0)fac.insert(i),fac.insert(a[n]/i);
    }
    int cnt,ans=g1;
    for(auto&f:fac){
        int mod=0;
        cnt=0;
        rep(i,2,n)if(b[i]%f!=0)cnt++,mod+=b[i]%f;
        if(cnt<=1){
            ans=max(ans,f);
        }
        if((cnt==2)&&(mod%f==0)){
            ans=max(ans,f);
        }
    }
    cout<<ans<<'\n';
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) { eachT(); }
}

---

D.漂亮矩阵

数学 #组合数 #广义二项式定理 #FFT

题目

思路

设\(B_{i,j}=A_{i,j+1}-A_{i,j}\)，则有\(B_{i,j}\geq B_{i+1,j}\)且\(\sum_{j=1}^nB_{i,j}\leq m\)

因此有\(\sum_{j=1}^nB_{i+1,j}\leq \sum_{j=1}^nB_{i,j}\leq \sum_{j=1}^nB_{1,j}\leq m\)

所以只需要满足\(\sum_{1,j}^nB_{1,j}\leq m\)且每列的\(B\)值单调不增即可

设\(B_{1,i}=x\)，一列共有\(n\)个元素，求这一列开头为\(x\)且后续单调不增的所有情况数：

• 假设有\(x\)块隔板\(l_{i},i\in[0,x]\)，若\(l_{i-1}\)到\(l_{i}\)间有\(k\)个数，则令这\(k\)个数为\(i\)
• 由于开头已经固定为\(x\)，只能对剩下的\(n-1\)个数进行操作，\(n-1\)个数提供\(n-1\)个空位，再加上\(x\)个隔板自己的位置，相当于一共\(x+n-1\)个空位中放入\(x\)个隔板，即\(C_{x+n-1}^x\)
  
  

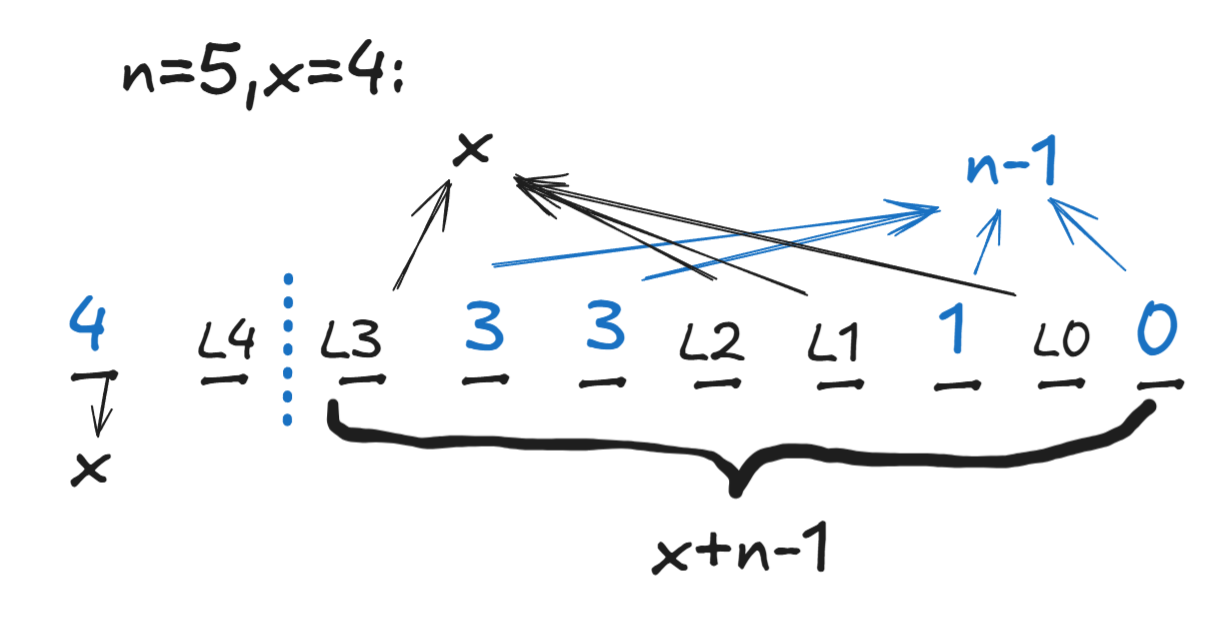
接下来利用生成函数来构造总和不超过\(m\)的所有情况数：

• 构造函数\(F(x)=C_{0+n-1}^0x^0+C_{1+n-1}^1x^1+\dots+C_{m+n-1}^mx^m+\dots=\sum_{i=0}^\infty C_{i+n-1}^ix^i\)
• 构造多项式\(F(x)·F(x)·\dots·F(x)=F(x)^{n-1}\)，相当于除了第一列以外的\(n-1\)列的所有情况。多项式\(F(x)^{n-1}\)中的前\(m\)项的系数之和即为总和不超过\(m\)的所有情况数

此时可以用\(FFT\)来快速得出答案，复杂度\(o(n\log n)\)

但是其实还可以用广义二项式定理进一步化简：

广义二项式定理实际上就是将组合数的定义域拓宽到了整个实数域

\[\begin{align}
&F(x)=\sum_{i=0}^\infty C_{i+n-1}^ix^i=(1-x)^{-n}\ \ \ (广义二项式定理)\\ \\
&F(x)^{n-1}=(1-x)^{-n(n-1)}\\ \\
&令t=n(n-1) \\ \\
&则F(x)^{n-1}=(1-x)^{-t} =\sum_{i=0}^\infty C_{i+t-1}^ix^i=\sum_{i=0}^\infty C_{i+t-1}^{t-1}x^i\\ \\
&则其前m项的系数和为\sum_{i=0}^mC_{i+t-1}^{t-1}=C_{m+t}^t\\ \\
&即求 \frac{(m+t)!}{t!·m!}= \frac{(m+t)(m+t-1)···(t+1)}{m!}
\end{align}
\]

分子可以\(o(m)\)暴力算出，分母可以\(o(m)\)预处理逆元算出，总复杂度为\(o(m)\)

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
#include<unordered_map>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i ++)
#define per(i, a, b) for(ll i = (a); i >= (b); i --)
//#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
const ll inf = 1e7 + 5;
// #define int ll
const int N=1e5+5;

ll mod=998244353;
ll qpow(ll a, ll b) {
	a %= mod; ll res = 1;
	while (b) {
		if (b % 2) { res *= a, res %= mod; }
		a *= a, a %= mod, b /= 2;
	}
	return res%mod;
}
vector<ll>a, inv;
void inv0(ll len) {
	a.resize(len + 1), inv.resize(len + 1);
	a[0] = 1, inv[0] = 1;
	rep(i, 1, len) {
		a[i] = a[i - 1] * i % mod;
		inv[i] = qpow(a[i], mod - 2);
	}
}

void eachT() {
    ll n,m;cin>>n>>m;
    ll ans=1;
    rep(i,1,m){
        ans*=(n*(n-1)+i)%mod;
        ans%=mod;
    }
    ans*=inv[m];
    ans%=mod;
    cout<<ans<<'\n';
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    inv0(5e5);
    ll t = 1;
    //cin >> t;
    while (t--) { eachT(); }
}