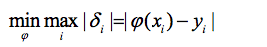最小二乘法多项式曲线拟合原理与实现 zz
概念
最小二乘法多项式曲线拟合,根据给定的m个点,并不要求这条曲线精确地经过这些点,而是曲线y=f(x)的近似曲线y= φ(x)。
原理
[原理部分由个人根据互联网上的资料进行总结,希望对大家能有用]
给定数据点pi(xi,yi),其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y,i=1,2,...,m。
常见的曲线拟合方法:
1.使偏差绝对值之和最小
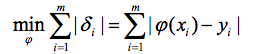
2.使偏差绝对值最大的最小
3.使偏差平方和最小
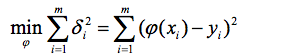
按偏差平方和最小的原则选取拟合曲线,并且采取二项式方程为拟合曲线的方法,称为最小二乘法。
推导过程:
1. 设拟合多项式为:

2. 各点到这条曲线的距离之和,即偏差平方和如下:
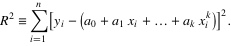

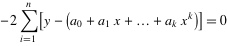
.......
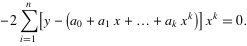
4. 将等式左边进行一下化简,然后应该可以得到下面的等式:
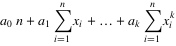
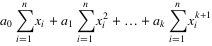
.......
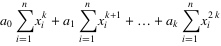
5. 把这些等式表示成矩阵的形式,就可以得到下面的矩阵:
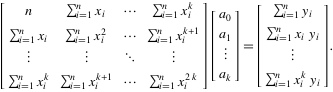
6. 将这个范德蒙得矩阵化简后可得到:

7. 也就是说
运行前提:
- Python运行环境与编辑环境;
- Matplotlib.pyplot图形库,可用于快速绘制2D图表,与matlab中的plot命令类似,而且用法也基本相同。
代码:
- # coding=utf-8
- '''''
- 作者:Jairus Chan
- 程序:多项式曲线拟合算法
- '''
- import matplotlib.pyplot as plt
- import math
- import numpy
- import random
- fig = plt.figure()
- ax = fig.add_subplot(111)
- #阶数为9阶
- order=9
- #生成曲线上的各个点
- x = numpy.arange(-1,1,0.02)
- y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x]
- #ax.plot(x,y,color='r',linestyle='-',marker='')
- #,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5"
- #生成的曲线上的各个点偏移一下,并放入到xa,ya中去
- i=0
- xa=[]
- ya=[]
- for xx in x:
- yy=y[i]
- d=float(random.randint(60,140))/100
- #ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')
- i+=1
- xa.append(xx*d)
- ya.append(yy*d)
- '''''for i in range(0,5):
- xx=float(random.randint(-100,100))/100
- yy=float(random.randint(-60,60))/100
- xa.append(xx)
- ya.append(yy)'''
- ax.plot(xa,ya,color='m',linestyle='',marker='.')
- #进行曲线拟合
- matA=[]
- for i in range(0,order+1):
- matA1=[]
- for j in range(0,order+1):
- tx=0.0
- for k in range(0,len(xa)):
- dx=1.0
- for l in range(0,j+i):
- dx=dx*xa[k]
- tx+=dx
- matA1.append(tx)
- matA.append(matA1)
- #print(len(xa))
- #print(matA[0][0])
- matA=numpy.array(matA)
- matB=[]
- for i in range(0,order+1):
- ty=0.0
- for k in range(0,len(xa)):
- dy=1.0
- for l in range(0,i):
- dy=dy*xa[k]
- ty+=ya[k]*dy
- matB.append(ty)
- matB=numpy.array(matB)
- matAA=numpy.linalg.solve(matA,matB)
- #画出拟合后的曲线
- #print(matAA)
- xxa= numpy.arange(-1,1.06,0.01)
- yya=[]
- for i in range(0,len(xxa)):
- yy=0.0
- for j in range(0,order+1):
- dy=1.0
- for k in range(0,j):
- dy*=xxa[i]
- dy*=matAA[j]
- yy+=dy
- yya.append(yy)
- ax.plot(xxa,yya,color='g',linestyle='-',marker='')
- ax.legend()
- plt.show()
运行效果:
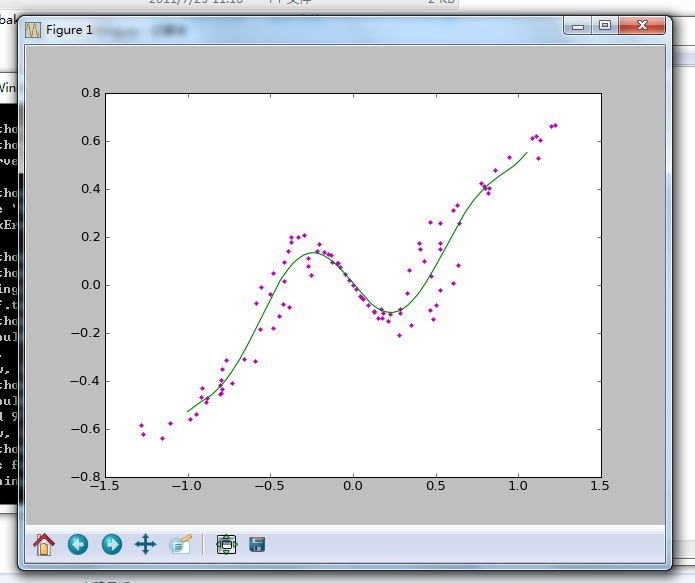
本博客中所有的博文都为笔者(Jairus Chan)原创。
如需转载,请标明出处:http://blog.csdn.net/JairusChan。
如果您对本文有任何的意见与建议,请联系笔者(JairusChan)。
最小二乘法多项式曲线拟合原理与实现 zz的更多相关文章
- 最小二乘法多项式拟合的Java实现
背景 由项目中需要根据一些已有数据学习出一个y=ax+b的一元二项式,给定了x,y的一些样本数据,通过梯度下降或最小二乘法做多项式拟合得到a.b,解决该问题时,首先想到的是通过spark mllib去 ...
- Apache Commons Math3学习笔记(2) - 多项式曲线拟合(转)
多项式曲线拟合:org.apache.commons.math3.fitting.PolynomialCurveFitter类. 用法示例代码: // ... 创建并初始化输入数据: double[] ...
- polyfit 多项式曲线拟合matlab
polyfit 多项式曲线拟合 全页折叠 语法 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n) 说明 示例 ...
- Numpy实现多项式曲线拟合
Numpy实现多项式曲线拟合 这里可以对比matlab中的拟合方式看看matlab拟合函数的三种方法,和第一种方式很像 问题定义:对于一堆数据点(x, y),能否只根据这些数据,找出一个函数,使得函数 ...
- 一起啃PRML - 1.1 Example: Polynomial Curve Fitting 多项式曲线拟合
一起啃PRML - 1.1 Example: Polynomial Curve Fitting @copyright 转载请注明出处 http://www.cnblogs.com/chxer/ 前言: ...
- 硬盘内部硬件结构和工作原理详解[zz]
一般硬盘正面贴有产品标签,主要包括厂家信息和产品信息,如商标.型号.序列号.生产日期.容量.参数和主从设置方法等.这些信息是正确使用硬盘的基本依据,下面将逐步介绍它们的含义. 硬盘主要由盘体.控制电路 ...
- 数据拟合:多项式拟合polynomial curve fitting
http://blog.csdn.net/pipisorry/article/details/49804441 常见的曲线拟合方法 1.使偏差绝对值之和最小 2.使偏差绝对值最大的最小 3 ...
- 算法+OpenCV】基于opencv的直线和曲线拟合与绘制(最小二乘法)
http://blog.csdn.net/guduruyu/article/details/72866144 最小二乘法多项式曲线拟合,是常见的曲线拟合方法,有着广泛的应用,这里在借鉴最小二乘多项式曲 ...
- 基于MATLAB的多项式数据拟合方法研究-毕业论文
摘要:本论文先介绍了多项式数据拟合的相关背景,以及对整个课题做了一个完整的认识.接下来对拟合模型,多项式数学原理进行了详细的讲解,通过对文献的阅读以及自己的知识积累对原理有了一个系统的认识.介绍多项式 ...
随机推荐
- 菜鸟nginx源码剖析
菜鸟nginx源码剖析 配置与部署篇(一) 手把手配置nginx "I love you" TCMalloc 对MYSQL 性能 优化的分析 菜鸟nginx源码剖析系列文章解读 A ...
- ==与equals与hashCode的区别联系。
前言:对于引用类型的变量,它涉及到两块内存,一块是堆中的内存,用于存放new出来的对象(就是对象的具体内容):另一块是栈内存,用来存放变量在堆内存中的地址. 1,“==” 判断两个变量是否是同一个变量 ...
- .babelrc文件的一些简单的配置
首先现在根目录先生存.babelrc文件 这个文件是用来设置转码的规则和插件的 如果想使用es6语法,必须安装插件 npm install babel-preset-es2015 { "pr ...
- 刚刚看到 PNaCl, 这才是我一直期待的跨平台的好东西!
http://code.google.com/p/nativeclient/ https://developers.google.com/native-client/overview
- MikroTik RouterOS安装后初始化配置(PPPOE拨号上网)
1.修改登入密码 路由器默认登入账号为admin,密码为空,强烈建议修改登入密码保证安全: 2.修改接口名称 选择Interface,切换到Ethernet标签,找到状态是R(run)的两个端口. 给 ...
- dotNetSpider 手记
准备工作: 从github上download工程. 安装VS2017. 安装 .net core 2.0. 编译通过. 基础架构: 调度器 Scheduler 从根site开始,向 Downloade ...
- VS2008 LINK : fatal error LNK1104: cannot open file 'atls.lib'错误解决方案
用VS 2008编写ATL的64位应用程序时,提示链接错误:VS2008 LINK : fatal error LNK1104: cannot open file 'atls.lib' 问题原因 VS ...
- DIOCP数据包太大,请在业务层分拆发送
DIOCP数据包太大,请在业务层分拆发送 DIOCP日志记录异常:数据包太大,请在业务层分拆发送...... 跟踪发现,原因在下图:
- 【Devops】【docker】【CI/CD】jenkins源码管理,添加SSH地址后报错+Jenkins构建报错:Please make sure you have the correct access rights and the repository exists.
jenkins源码管理,添加SSH地址后报错: Could not read from remote repository. Please make sure you have the correct ...
- 技术人生:special considerations that are very important
For the most part, a lot of what we know about software development can be applied to different envi ...