机器学习入门-主成分分析(PCA)

主成分分析：

用途：降维中最常用的一种方法

目标：提取有用的信息(基于方差的大小)

存在的问题：降维后的数据将失去原本的数据意义

向量的内积：A*B = |A|*|B|*cos(a) 如果|B| = 1，那么A*B = |A| * cos(a) 即在B的方向上对A做投影

基变化: 如果向量为(3, 2)那么它可以有(1, 0)和(0, 1)一组基进行表示，这两个基是正交的

在基变化过程中，每一个基都是正交的即线性无关

数据与第一个基进行内积，形成一个新的分量，数据与第二个基做内积，形成第二个分量，由于基是正交的，而内积表示的是投影，因此这两个分量也是正交的

即 1/m ai.dot(bi) = 0。

方差：变量的方差越大，其分散程度也就越大，方差 (ai-ui).dot((ai-ui).T) ui表示的是样本的均值

协方差：两个向量的内积，协方差越小，表示两个向量越不相似cov(a, b) = 1/m*(a.dot(b.T))

引入协方差的目的:

如果单纯只看变化后的方差大小，那么求得的基可能都在方差最大的方向附件进行徘徊，因为我们为了使变换后的特征尽可能的表示原始信息，我们使得变化后的特征是正交的情况，即特征之间线性无关，协方差cov=0

结合上述的两个条件：第一：变换后的矩阵的方差最大1/m ai.dot(ai.T)

第二：变换后的矩阵的协方差等于0  1/m ai.dot(bi.T)

我们引入了协方差矩阵，协方差矩阵对角线是方差，非对角线上是协方差

公式： 1/m X.dot(X.T)

1/m * Y.dot(Y.T) = 1/m PX.dot((PX).T) = 1/m(P* X * X^T * P^T)

令上面的式子中的 X*X^T等于C,那么上面的式子就是 1/m * Y.dot(Y.T) = 1/m(P* C * P^T)

我们需要使得1/m * Y.dot(Y.T) 满足上述两个条件，即对C做一个对角化变化，使得变化后的矩阵对角线上的表示方差(从大到小排列)， 非对角线上等于0

这个问题前人已经研究了很透，即上述变化的P就是C的特征向量，而C等于X*X^T

我们只需要求得X*X^T的特征向量即可

上述的过程的实现步骤：

1.对特征进行标准化

2.去均值

3.求协方差矩阵 X*X^T

4.协方差矩阵的特征向量

5.使用前几维的特征向量与特征进行内积，实现特征降维

代码：

第一步：导入数据， 进行列名赋值

第二步：提取特征和标签

第三步：对每一个特征进行物体类别画直方图，研究不同变量对特征分布的影响

第四步：对样本特征进行标准化操作

第五步：对样本去均值并构造协方差矩阵X.dot(X.T)

第六步：对构造好的协方差矩阵求特征值和特征向量

第七步：将求得的特征值和特征向量进行组合， 对组合的特征进行排序操作，将排序后的特征进行使用np.cumsum对特征值进行加和

第八步：使用条形图和步进图对特征值和加和后的特征进行作图操作

第九步：选取前两个特征向量与标准化后的特征进行内积操作，获得降维后的特征

第十步：对降维后的特征画出散点图

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 第一步 数据读取
data = pd.read_csv('iris.data')

data.columns = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'classes']

# 第二步 提取特征
X = data[['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid']].values
y = data['classes'].values

feature_names = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid']
label_names = data['classes'].unique()

# 第三步 对每一个特征的样品类别做直方图
for feature in range(len(feature_names)):
    plt.subplot(2, 2, feature+1)
    for label in label_names:
        plt.hist(X[y==label, feature], bins=10, alpha=0.5, label=label)
    plt.legend(loc='best')
plt.show()

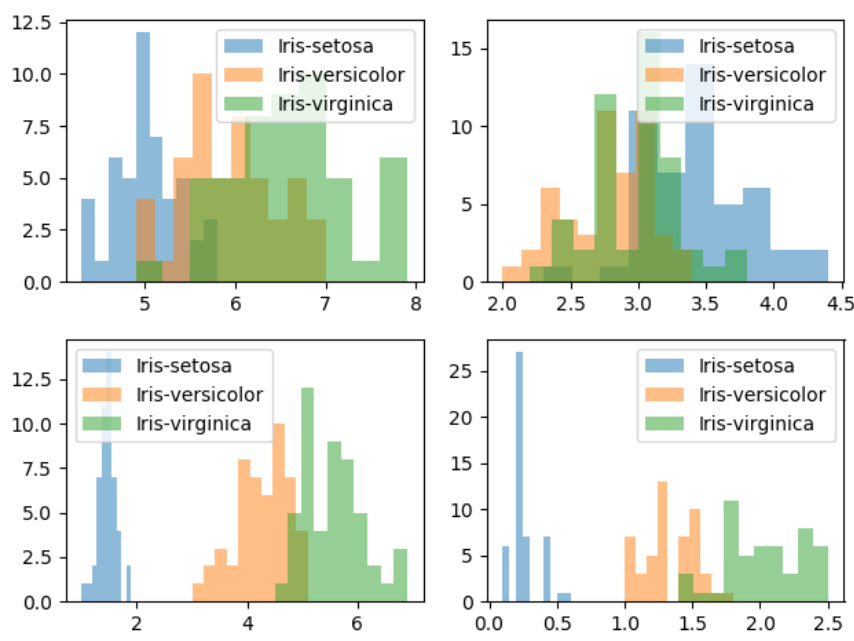
不同变量对类别分布的影响

# 第四步 对特征进行标准化操作
from sklearn.preprocessing import StandardScaler

std_feature = StandardScaler().fit_transform(X)

# 第五步 对特征去除均值, 并构造协方差矩阵, 也可以使用np.conv进行构造
mean_fea = std_feature.mean(axis=0)
cov_matrix = (std_feature - mean_fea).T.dot(std_feature-mean_fea)

# 第六步 使用np.linalg.eig 求出协方差矩阵的特征值和特征向量

eig_val, eig_vector = np.linalg.eig(cov_matrix)

# 第七步：我们将特征值和特征向量进行组合

eig_paries = [(eig_val[j], eig_vector[:, j]) for j in range(len(eig_val))]

# 获得对组合的特征值进行排序，获得重要性的占比
sum_val = np.sum(eig_val)
feature_importance = [eig_v[0]/sum_val * 100 for eig_v in sorted(eig_paries, key=lambda x:x[0], reverse=True)]
print(feature_importance)
# 使用np.cumsum进行两两的前后加和
su_feature_importance = np.cumsum(feature_importance)
# 第八步：对特征重要性进行作图操作
figure = plt.figure(figsize=(8, 6))
plt.bar(range(4), feature_importance, align='center', label='identity explain variance', alpha=0.5)
# plt.step表示的是步进图， where表示的线条的表示方式
plt.step(range(4), su_feature_importance, where='mid', label='cumidentity explain variance')
plt.xlabel('PC component')
plt.ylabel('variance importance')
plt.show()

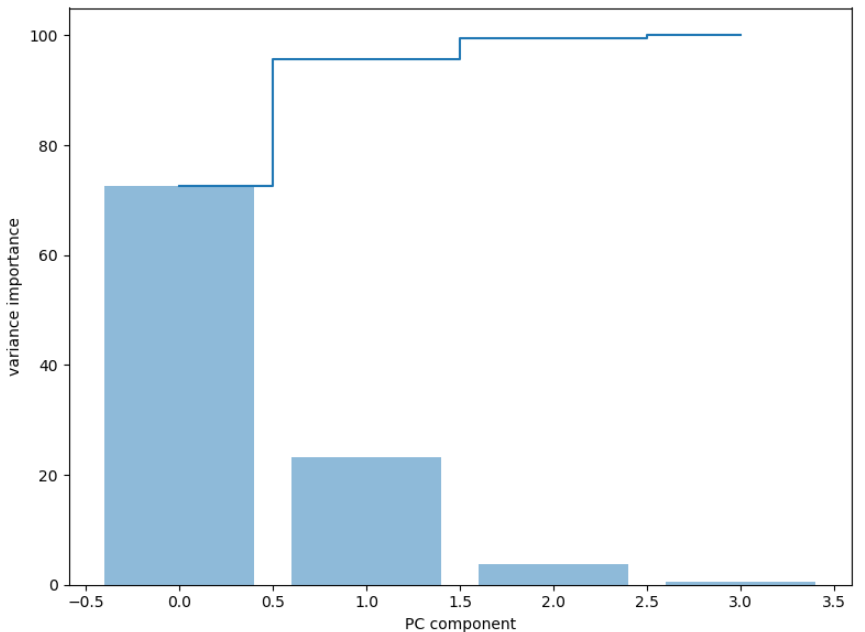
特征值重要比例图

# 第九步：使用前两个特征向量进行矩阵的变换

eig_vector_two = np.vstack([eig_paries[0][1], eig_paries[1][1]])
trans_std_X = std_feature.dot(eig_vector_two.T)

# 第十步： 对变化后的数据进行画图操作

figure = plt.figure(figsize=(8, 6))
for label, c in zip(label_names, ['red', 'green', 'black']):
    plt.scatter(std_feature[y==label][:, 0], std_feature[y==label][:, 1], c=c, label=label, alpha=0.6, s=20)
    leg = plt.legend(loc='best')
    leg.get_frame().set_alpha(0.6)
    plt.xlabel(feature_names[0])
    plt.ylabel(feature_names[1])
plt.show()

figure = plt.figure(figsize=(8, 6))
for label, c in zip(label_names, ['red', 'green', 'black']):
    plt.scatter(trans_std_X[y==label][:, 0], trans_std_X[y==label][:, 1], c=c, label=label, alpha=0.6, s=20)
    leg = plt.legend(loc='best')
    leg.get_frame().set_alpha(0.6)
    plt.xlabel('PC1')
    plt.ylabel('PC2')
plt.show()

原始特征图                                                               降维后的特征图