正定矩阵(Positive-definite Matrix)
正定矩阵是自共轭矩阵的一种。正定矩阵类似复数中的正实数。定义:对于对称矩阵M,当且仅当存在任意向量x,都有
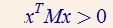
若上式大于等于零,则称M为半正定矩阵。正定矩阵记为M>0。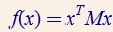
也被称为正定二次型
正定矩阵的判定
1、所有特征值为正数(根据谱定理,若条件成立,必然可以找到对角矩阵的D和正定矩阵P,使M=P^-1DP);
2、所有的顺序主子式为正定;
3、Cholesky分解得到的矩阵,其主对角线上的元素全为正数;
4、矩阵有半双线性映射形式。
首先解释双线性映射。假设三个向量空间X, Y和Z,有Z = B(X, Y)。对于X或Y中的任意向量都有到Z的唯一映射。如果把X固定,Y中的元素就存在到Z的线性映射,反过来也一样。
所谓半双线性映射,就是它的两个参数一个是线性的,另一个是半线性的(或共轭线性)。如: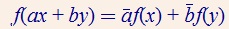
复数空间的内积都是半双线性的。
正定矩阵的性质
1、正定矩阵均可逆,且逆矩阵也为正定矩阵;
2、正定矩阵与正实数的乘积也为正定;
3、迹Tr(M)>0;
4、存在唯一的平方根矩阵B,使得: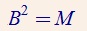
正定矩阵(Positive-definite Matrix)的更多相关文章
- 【线性代数】6-5:正定矩阵(Positive Definite Matrices)
title: [线性代数]6-5:正定矩阵(Positive Definite Matrices) categories: Mathematic Linear Algebra keywords: Po ...
- 正定矩阵(positive definite matrix)
设M是n阶方阵,如果对任何非零向量z,都有zTMz> 0,其中zT 表示z的转置,就称M正定矩阵. 正定矩阵在合同变换下可化为标准型, 即对角矩阵. 所有特征值大于零的对称矩阵也是正定矩阵. ...
- 正定矩阵(definite matrix)
1. 基本定义 在线性规划中,一个对称的 n×n 的实值矩阵 M,如果满足对于任意的非零列向量 z,都有 zTMz>0. 更一般地,对于 n×n 的 Hermitian 矩阵(原矩阵=共轭转置, ...
- a positive definite matrix
https://en.wikipedia.org/wiki/Definite_quadratic_form https://www.math.utah.edu/~zwick/Classes/Fall2 ...
- Cholesky分解 平方根法
一种矩阵运算方法,又叫Cholesky分解.所谓平方根法,就是利用对称正定矩阵的三角分解得到的求解对称正定方程组的一种有效方法.它是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解.它要 ...
- cholesky分解
接着LU分解继续往下,就会发展出很多相关但是并不完全一样的矩阵分解,最后对于对称正定矩阵,我们则可以给出非常有用的cholesky分解.这些分解的来源就在于矩阵本身存在的特殊的 结构.对于矩阵 ...
- 从线性模型(linear model)衍生出的机器学习分类器(classifier)
1. 线性模型简介 0x1:线性模型的现实意义 在一个理想的连续世界中,任何非线性的东西都可以被线性的东西来拟合(参考Taylor Expansion公式),所以理论上线性模型可以模拟物理世界中的绝大 ...
- AI人工智能专业词汇集
作为最早关注人工智能技术的媒体,机器之心在编译国外技术博客.论文.专家观点等内容上已经积累了超过两年多的经验.期间,从无到有,机器之心的编译团队一直在积累专业词汇.虽然有很多的文章因为专业性我们没能尽 ...
- [C9] 降维(Dimensionality Reduction)
降维(Dimensionality Reduction) 动机一:数据压缩(Motivation I : Data Compression) 数据压缩允许我们压缩数据,从而使用较少的计算机内存或磁盘空 ...
- Mahout 系列之----共轭梯度
无预处理共轭梯度 要求解线性方程组 ,稳定双共轭梯度法从初始解 开始按以下步骤迭代: 任意选择向量 使得 ,例如, 对 若 足够精确则退出 预处理共轭梯度 预处理通常被用来加速迭代方法的收敛.要使用预 ...
随机推荐
- JAVA生成word的几种方法对比
首先介绍几种java导出word方案 1.Jacob是Java-COM Bridge的缩写,它在Java与微软的COM组件之间构建一座桥梁.使用Jacob自带的DLL动态链接库,并通过JNI的方式实现 ...
- Spark为什么比Hadoop好?
(1)Spark计算速度远胜于Hadoop的原因之一就在于中间结果是缓存在内存而不是直接写入到disk Hadoop每次计算先写磁盘,下次计算先从磁盘读,计算结果再写磁盘,如此往复.这对于迭代计算,是 ...
- LISP语言学习资源
LISP的介绍:Paul Graham 的主页 http://paulgraham.com/index.html Lisp之根源 - 保罗·格雷厄姆 http://daiyuwen.freeshell ...
- 关于数学问题的urls
一个知乎账号, 分析了很多的数学问题: https://www.zhihu.com/people/matongxue/activities 关于三阶样条的解析: https://blog.csdn.n ...
- Jquery 客户端验证
Jquery 客户端验证 //引入js文件 validate.js <html> <head> <title>jqueryValidateDemo</titl ...
- [Java][Liferay] 如何从Javascript的function中获取language property的值
问题描述 在Portlet中,Javascript中通过Liferay.Language.get("key")的方式是拿不到自己添加的property的值,原因是Liferay.L ...
- hdu 3586 最小代价切断根与叶子联系
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3586 http://blog.csdn.net/woshi250hua/article/details ...
- ACM-单调队列
对于单调队列的基本概念可以去看百科里的相关介绍:http://baike.baidu.com/view/3771451.htm 这里挑一些重点. 作用: 不断地向缓存数组里读入元素,也不时地去掉最老的 ...
- 为什么要使用markdown?
markdown是什么? markdown是一种标记语言,它不是编程语言 为什么要使用markdown? markdown可以使用任何文本编辑器编写和查看 markdown编写的文件可以转化为html ...
- IE浏览器在线更新GitHub客户端
在IE中输入网址:http://github-windows.s3.amazonaws.com/GitHub.application
