【复杂度分析】loj#6043. 「雅礼集训 2017 Day7」蛐蛐国的修墙方案

感觉有点假

题目大意

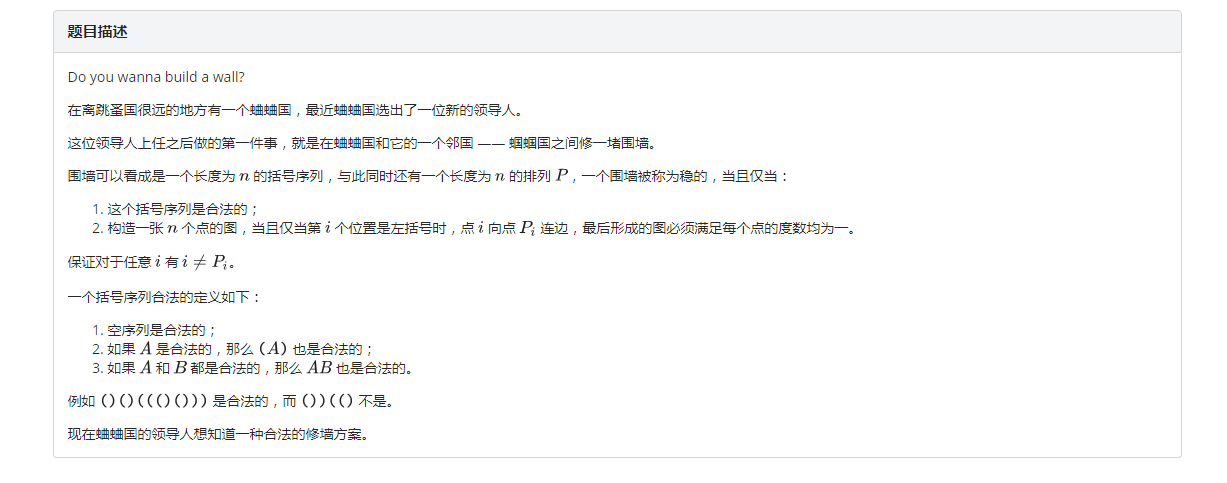
数据范围：$n<=100$

---

题目分析

由于题目给出的是 置换，所以相当于只需枚举每个环的两个状态。

主要是复杂度分析这里：

一元环：不存在

二元环：特判保平安

三元环：不存在

四元环：复杂度$O(2^{25})$，但是特判一下顺序就可以秒下来了

六元环：复杂度$O(2^{17})$至此及以后的复杂度都是可以接受的了

不知道为什么倒着搜就会更快？

 #include<bits/stdc++.h>
 const int maxn = ;

 int n,las,p[maxn],w[maxn],deg[maxn];

 void dfs(int x)
 {
     if (x==){
         if (las) return;
         for (int i=; i<=n; i++)
             putchar(w[i]?'(':')');
         exit();
     }
     if (w[x]!=-){
         int che = w[p[x]];
         if (w[p[x]]!=-&&((-w[x])!=w[p[x]])) return;
         w[p[x]] = -w[x];
         las -= w[x]?:-;
         if (las >= ) dfs(x-);
         las += w[x]?:-;
         w[p[x]] = che;
     }else{
         w[x] = ;
         int che = w[p[x]], chk = ;
         for (int i=p[x],f=w[x]; i!=x; i=p[i])
             f = -f, chk &= (w[i]==-)||(f==w[i]);
         if (chk){
             int bck[maxn],bct = ;
             for (int i=p[x],f=w[x]; i!=x; i=p[i])
                 f = -f, bck[++bct] = w[i], w[i] = f;
             las -= w[x]?:-;
             if (las >= ) dfs(x-);
             las += w[x]?:-;
             for (int i=p[x],f=; i!=x; i=p[i])
                 w[i] = bck[f], ++f;
         }

         w[x] = ;
         che = w[p[x]];
         if (w[p[x]]==-||((-w[x])==w[p[x]])){
             w[p[x]] = -w[x];
             las -= w[x]?:-;
             if (las >= ) dfs(x-);
             las += w[x]?:-;
             w[p[x]] = che;
         }

         w[x] = -;
     }
 }
 int main()
 {
     memset(w, -, sizeof w);
     scanf("%d",&n);
     for (int i=; i<=n; i++) scanf("%d",&p[i]), ++deg[p[i]];
     dfs(n);
     return ;
 }

END