Hessian矩阵【转】

http://blog.sina.com.cn/s/blog_7e1ecaf30100wgfw.html

在数学中，海塞矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵，一元函数就是二阶导，多元函数就是二阶偏导组成的矩阵。求向量函数最小值时可以使用，矩阵正定是最小值存在的充分条件。经济学中常常遇到求最优的问题，目标函数是多元非线性函数的极值问题，尚无一般的求解方法，但判定局部极小值的方法就是用hessian矩阵：

在x0点上，hessian矩阵是负定的，且各分量的一阶偏导数为0，则x0为极大值点。

在x0点上，hessian矩阵式正定的，且各分量的一阶偏导数为0，则x0为极小值点。

矩阵是负定的充要条件是各个特征值均为负数。

矩阵是正定的充要条件是各个特征值均为正数。

函数如下：

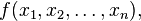
如果f所有的二阶导数都存在，那么f的海塞矩阵即为：H(f)_ij(x) = D_iD_jf(x)，即

（也有人把海色定义为以上矩阵的行列式）海赛矩阵被应用于牛顿法解决的大规模优化问题。

性质

对称性：如果函数f在D区域内二阶连续可导，那么f海塞矩阵H（f）在D内为对称矩阵。原因是：如果函数f连续，则二阶偏导数的求导顺序没有区别，即：

则对于海塞矩阵H（f）,有，所以为对称矩阵。

多元函数极值的判定

如果实值多元函数二阶连续可导，并且在临界点M(x_i)(其中i=1,2,...,n，并且X_i已知)处梯度（一阶导数）等于0，即，则M为驻点。仅通过一阶导数无法判断在临界点M处是极大值还是极小值。

记f在M点处的黑塞矩阵为H(M)。由于f在M点处连续，所以H(M)是一个的对称矩阵，对于H(M),由如下结论：

• 如果H(M)是正定矩阵，则临界点M处是一个局部的极小值。
• 如果H(M)是负定矩阵，则临界点M处是一个局部的极大值。
• 如果H(M)是不定矩阵，则临界点M处不是极值。