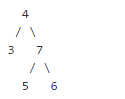LintCode-88.最近公共祖先
最近公共祖先
给定一棵二叉树,找到两个节点的最近公共父节点(LCA)。
最近公共祖先是两个节点的公共的祖先节点且具有最大深度。注意事项
假设给出的两个节点都在树中存在
样例
对于下面这棵二叉树
LCA(3, 5) = 4
LCA(5, 6) = 7
LCA(6, 7) = 7标签
LintCode 版权所有 领英 二叉树 脸书
code
/**
* Definition of TreeNode:
* class TreeNode {
* public:
* int val;
* TreeNode *left, *right;
* TreeNode(int val) {
* this->val = val;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
public:
/**
* @param root: The root of the binary search tree.
* @param A and B: two nodes in a Binary.
* @return: Return the least common ancestor(LCA) of the two nodes.
*/
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *A, TreeNode *B) {
// write your code here
TreeNode * ancestor = NULL;
if(root==NULL || A==NULL || B==NULL)
return ancestor;
vector<TreeNode *> pathA, pathB;
searchTree(root, A, pathA);
searchTree(root, B, pathB);
int sizeA=pathA.size(), sizeB=pathB.size();
int size = sizeA>sizeB ? sizeB : sizeA, i=0;
bool find = false;
for(i=0; i<size; i++) {
if(pathA[i] != pathB[i]) {
find = true;
return ancestor;
}
else
ancestor = pathA[i];
}
if(find == false)
ancestor = pathA[size-1];
return ancestor;
}
bool searchTree(TreeNode *root, TreeNode *node, vector<TreeNode *> &path) {
if(root==NULL || node==NULL) {
return false;
}
path.push_back(root);
// 找到了
if(root->val == node->val) {
return true;
}
if(root->left != NULL) {
if(searchTree(root->left, node, path)) {
return true;
}
}
if(root->right != NULL) {
if(searchTree(root->right, node, path)) {
return true;
}
}
//回溯
path.pop_back();
return false;
}
};LintCode-88.最近公共祖先的更多相关文章
- lintcode :最近公共祖先
题目 最近公共祖先 给定一棵二叉树,找到两个节点的最近公共父节点(LCA). 最近公共祖先是两个节点的公共的祖先节点且具有最大深度. 样例 对于下面这棵二叉树 4 / \ 3 7 / \ 5 6 LC ...
- LintCode 近期公共祖先
中等 近期公共祖先 查看执行结果 34% 通过 给定一棵二叉树,找到两个节点的近期公共父节点(LCA). 近期公共祖先是两个节点的公共的祖先节点且具有最大深度. 您在真实的面试中是否遇到过这个题? Y ...
- 《剑指offer》面试题68 - II. 二叉树的最近公共祖先
问题描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先. 百度百科中最近公共祖先的定义为:"对于有根树 T 的两个结点 p.q,最近公共祖先表示为一个结点 x,满足 x 是 p.q ...
- LCA最近公共祖先 ST+RMQ在线算法
对于一类题目,是一棵树或者森林,有多次查询,求2点间的距离,可以用LCA来解决. 这一类的问题有2中解决方法.第一种就是tarjan的离线算法,还有一中是基于ST算法的在线算法.复杂度都是O( ...
- 【转】最近公共祖先(LCA)
基本概念 LCA:树上的最近公共祖先,对于有根树T的两个结点u.v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u.v的祖先且x的深度尽可能大. RMQ:区间最小值查询问题.对于长度为n的 ...
- 【并查集】【树】最近公共祖先LCA-Tarjan算法
最近公共祖先LCA 双链BT 如果每个结点都有一个指针指向它的父结点,于是我们可以从任何一个结点出发,得到一个到达树根结点的单向链表.因此这个问题转换为两个单向链表的第一个公共结点(先分别遍历两个链表 ...
- 洛谷P3379 【模板】最近公共祖先(LCA)
P3379 [模板]最近公共祖先(LCA) 152通过 532提交 题目提供者HansBug 标签 难度普及+/提高 提交 讨论 题解 最新讨论 为什么还是超时.... 倍增怎么70!!题解好像有 ...
- Tarjan应用:求割点/桥/缩点/强连通分量/双连通分量/LCA(最近公共祖先)【转】【修改】
一.基本概念: 1.割点:若删掉某点后,原连通图分裂为多个子图,则称该点为割点. 2.割点集合:在一个无向连通图中,如果有一个顶点集合,删除这个顶点集合,以及这个集合中所有顶点相关联的边以后,原图变成 ...
- 数据结构作业——sights(最短路/最近公共祖先)
sights Description 美丽的小风姑娘打算去旅游散心,她走进了一座山,发现这座山有 n 个景点,由于山路难修,所以施工队只修了最少条的路,来保证 n 个景点联通,娇弱的小风姑娘不想走那么 ...
随机推荐
- [].slice.call的理解
首先要说明[].slice.call()与Array.prototype.slice.call() 有什么区别? [].slice === Array.prototype.slice true []为 ...
- 初识Pentaho(一)
学习一门语言或工具,首先得知道该工具的用途是什么.Pentaho 的官方定义是一个集数据集成和数据分析于一体的平台.这样的解释还是有点模糊.还是看其有哪些特点吧: ☐可以进行数据集成.谈到数据集成这 ...
- Linux的数据传输
1. sz 与 rz sz:将选定的文件从本地发送(send)到远端机器 rz:运行该命令会弹出一个文件选择窗口,从本地选择文件夹,接收(receive)从远端的文件 mac 下使用 brew 安装: ...
- Linux C语言编程基本原理与实践
Linux C语言编程基本原理与实践(2018-06-16 19:12:15) Linux C语言编程基本原理与实践 高效的学习带着目的性: 是什么 -> 干什么 -> 怎么用 重识C语言 ...
- javascript sorting/ v8 sorting
https://github.com/mgechev/v8-sorting-test/tree/master/src/algorithms
- CodeForces 547D Mike and Fish 思维
题意: 二维平面上给出\(n\)个点,然后对每个点进行染色:红色和蓝色,要求位于同一行或同一列的点中,红色点和蓝色点的个数相差不超过1 分析: 正解是求欧拉路径,在这篇博客中看到一个巧妙的思路: 对于 ...
- P1803 凌乱的yyy
P1803 凌乱的yyy 题目背景 快noip了,yyy很紧张! 题目描述 现在各大oj上有n个比赛,每个比赛的开始.结束的时间点是知道的. yyy认为,参加越多的比赛,noip就能考的越好(假的) ...
- iOS 中的正则表达式符号
最近重新看了一遍 iOS 的正则文档,简单翻译下文档中涉及到的符号 1.正则表达式元字符 符号 说明 \a 响铃, \u0007 \A 匹配输入的开始,只匹配第一行,也就是忽略多行选项 \b 不在[] ...
- Jsp刷新分页模板,很全
1.用来实现上一页下一页,我直接写到查询页面上 <%--page的分页--%> <style type="text/css"> a { color: # ...
- nodejs 文件系统
nodejs访问文件系统 所有的文件系统的调用,都需要加载fs模块,即var fs=require('fs'); nodejs提供的fs模块几乎所有的功能都有两种形式选择:异步和同步,如异步的wr ...