最小生成树（Kruskal和Prim算法）

关于图的几个概念定义：

        

关于图的几个概念定义：

• 连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。
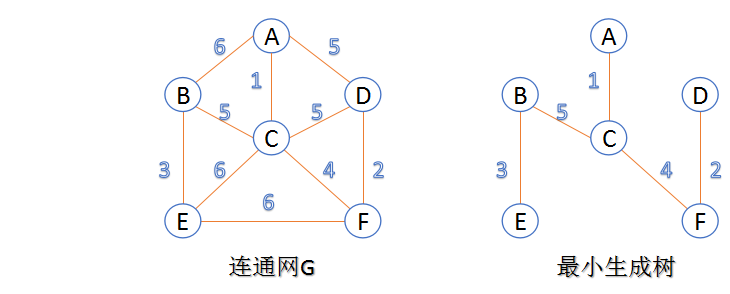
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
• 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

构造最小生成树的准则有3条：

（1）必须只使用该网络中的边来构造最小生成树。

（2）必须使用且仅使用n-1条边来连接网络中的n个顶点。

（3）不能使用产生回路的边。

---

下面介绍两种求最小生成树算法

1 Prim（普利姆算法）算法--加点法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中。Prim算法在找当前最近顶点时使用到了贪婪算法。

实现过程：

图例	说明	不可选	可选	已选（Vnew）
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

 #include<stdio.h>
 #include<string.h>
 #define MAX 0x3f3f3f3f
 using namespace std;
 int logo[];///用0和1来表示是否被选择过
 int map1[][];
 int dis[];///记录任意一点到这一点的最近的距离
 int n,m;
 int prim()
 {
     int i,j,now;
     int sum=;
     for(i=;i<=n;i++)///初始化
     {
         dis[i]=MAX;
         logo[i]=;
     }
     for(i=;i<=n;i++)
     {
         dis[i]=map1[][i];
     }
     dis[]=;
     logo[]=;
     for(i=;i<n;i++)///循环查找
     {
         now=MAX;
         int min1=MAX;
         for(j=;j<=n;j++)
         {
             if(logo[j]==&&dis[j]<min1)
             {
                 now=j;
                 min1=dis[j];
             }
         }
         if(now==MAX)///防止不成图
         {
             break;
         }
         logo[now]=;
         sum=sum+min1;
         for(j=;j<=n;j++)///填入新点后更新最小距离，到顶点集的距离
         {
             if(logo[j]==&&dis[j]>map1[now][j])
             {
                 dis[j]=map1[now][j];
             }
         }
     }
     if(i<n)
     {
         printf("?\n");
     }
     else
     {
         printf("%d\n",sum);
     }
 }
 int main()
 {
     while(scanf("%d%d",&m,&n)!=EOF)///n是点数
     {
         if(m==)
         {
             break;
         }
         memset(map1,0x3f3f3f3f,sizeof(map1));///map是邻接矩阵储存图的信息
         for(int i=;i<m;i++)
         {
             int a,b,c;
             scanf("%d%d%d",&a,&b,&c);
             if(c<map1[a][b])///防止出现重边
             {
                 map1[a][b]=map1[b][a]=c;
             }
         }
         prim();
     }
     return ;
 }

邻接表实现：

 #include<stdio.h>
 #include<string.h>
 #include<vector>
 #include<algorithm>
 #define INF 0x3f3f3f3f
 using namespace std;
 struct node
 {
     int end;///终点
     int power;///权值
 } t;
 int n;///n为点数
 vector<node>q[];///邻接表储存图的信息
 int dis[];///距离
 int vis[];///标记数组
 void  prime()
 {
     int i,len,j,pos,sum,start;
     memset(vis,,sizeof(vis));
     sum=;
     start=;///任意取起点
     for(i=; i<=n; i++)
     {
         dis[i]=INF;
     }
     len=q[start].size();
     for(i=; i<len; i++)///从任意起点开始的dis数组更新
     {
         if(q[start][i].power<dis[q[start][i].end])
         {
             dis[q[start][i].end]=q[start][i].power;
         }
     }
     vis[start]=;
     for(j=; j<n-; j++)
     {
         int pos,min=INF;
         for(i=; i<=n; i++)
         {
             if(vis[i]!=&&dis[i]<min)
             {
                 min=dis[i];
                 pos=i;///找到未访问节点中权值最小的
             }
         }
         if(pos==INF)///防止不成图
         {
             break;
         }
         vis[pos]=;
         sum=sum+min;
         len=q[pos].size();///再次更新dis数组
         for(j=; j<len; j++)
         {
             if(vis[q[pos][j].end]==&&dis[q[pos][j].end]>q[pos][j].power)
             {
                 dis[q[pos][j].end] = q[pos][j].power;
             }
         }
     }
     if(j<n)
     {
         printf("?\n");
     }
     else
     {
         printf("%d\n",sum);
     }
 }
 int main()
 {
     int m,i;
     int begin,end,power;
     int a,b;
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         for(i=; i<=n; i++)
         {
             q[i].clear();///将victor数组清空
         }
         for(i=; i<m; i++)
         {
             scanf("%d%d%d",&begin,&end,&power);///输入
             t.end=end;
             t.power=power;
             q[begin].push_back(t);
             t.end=begin;///无向图
             t.power=power;
             q[end].push_back(t);
         }
         prime();
     }
     return ;
 }

这里再给出一个没有使用标记数组的代码：

int prim(int s)
{
    int i,j,sum=;
    int now;
    for(i=;i<=n;i++)
    {
        closest[i]=INT_MAX;
    }
    for(i=;i<=n;i++)
    {
        closest[i]=map[s][i];
    }
    closest[s]=;
    for(i=;i<n;i++)//这里的i代表的是边数，有n个点就会有n-1条边
    {
        int min=INT_MAX;
        for(j=;j<=n;j++)
        {
            if(closest[j]&&closest[j]<min)
            {
                min=closest[j];
                now=j;//找到所需的最小边
            }
        }
        sum+=min;
        closest[now]=;//将找到的边加入到最小生成树之中
        for(j=;j<=n;j++)//找到新的点加入已选点集合之后，更新该点到未选点集合的距离
        {
            if(map[now][j]&&map[now][j]<closest[j])
            {
                closest[j]=map[now][j];
            }
        }
    }
    return sum;
}

2 Kruskal（克鲁斯卡尔）算法--加边法

1.概览

　　Kruskal算法是一种用来寻找最小生成树的算法，在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。

2.实现过程

1).记Graph中有v个顶点，e个边

2).新建图Graph_new，Graph_new中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从小到大排序

4).循环：从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中  if 这条边连接的两个节点于图Graph_new中不在同一个连通分量中   添加这条边到图Graph_new中

　　图例描述：

首先第一步，我们有一张图Graph，有若干点和边

将所有的边的长度排序，用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序，对局部最优的资源进行选择，排序完成后，我们率先选择了边AD。这样我们的图就变成了下图

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

依次类推我们找到了6,7,7，即DF，AB，BE。

下面继续选择， BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了（对于BC可以通过CE,EB来连接，类似的EF可以通过EB,BA,AD,DF来接连）。所以不需要选择他们。类似的BD也已经连通了（这里上图的连通线用红色表示了）。最后就剩下EG和FG了。当然我们选择了EG。

代码：（利用并查集来实现）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,sum;
struct node
{
    int start;///起点
    int end;///终点
    int power;///权值
}edge[];
int pre[];
int cmp(node a,node b)
{
    return a.power<b.power;///按权值排序
}
int Find(int x)///并查集找祖先
{
    if(x!=pre[x])///递归法
    {
        pre[x]=Find(pre[x]);
    }
    return pre[x];

    /*int a;///循环法
    a=x;
    while(pre[a]!=a)
    {
        a=pre[a];
    }
    return a;*/
}
void Union(int x,int y,int n)
{
    int fx =Find(x);
    int fy =Find(y);
    if(fx!=fy)
    {
        pre[fx]=fy;
        sum+=edge[n].power;
    }
}
int main()
{
    int i;
    while(scanf("%d",&n)!=EOF)
    {
        sum=;
        m=n*(n-)/;
        for(i=;i<=m;i++)
        {
            scanf("%d%d%d",&edge[i].start,&edge[i].end,&edge[i].power);
        }
        for(i=;i<=m;i++)///并查集的初始化
        {
            pre[i]=i;
        }
        sort(edge+,edge+m+,cmp);
        for(i=;i<=m;i++)
        {
            Union(edge[i].start,edge[i].end,i);
        }
        printf("%d\n",sum);
    }
    return ;
}