贪心：SPOJ Backup Files

BACKUP - Backup Files

no tags 

You run an IT company that backs up computer data for large offices. Backing up data is not fun, and so you design your system so that the different offices can back up each others' data while you sit at home and play computer games instead.

The offices are all situated along a single street. You decide to pair up the offices, and for each pair of offices you run a network cable between the two buildings so that they can back up each others' data.

However, network cables are expensive. Your local telecommunications company will only give you k network cables, which means you can only arrange backups for k pairs of offices (2k offices in total). No office may belong to more than one pair (that is, these 2k offices must all be different). Furthermore, the telecommunications company charges by the kilometre. This means that you need to choose these k pairs of offices so that you use as little cable as possible. In other words, you need to choose the pairs so that, when the distances between the two offices in each pair are added together, the total distance is as small as possible.

As an example, suppose you had five clients with offices on a street as illustrated below. These offices are situated 1 km, 3 km, 4 km, 6km and 12km from the beginning of the street. The telecommunications company will only provide you with k = 2 cables.

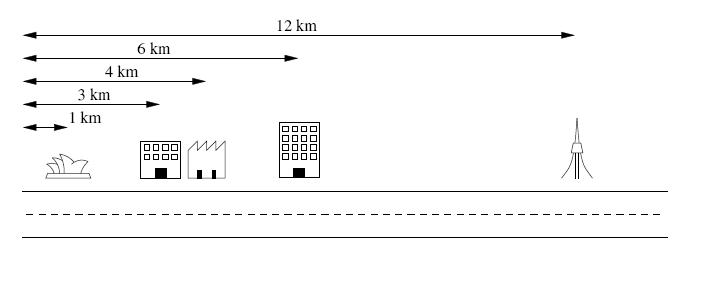
The best pairing in this example is created by linking the first and second offices together, and linking the third and fourth offices together. This uses k = 2 cables as required, where the first cable has length 3km - 1km = 2 km, and the second cable has length 6km - 4km = 2 km. This pairing requires a total of 4km of network cables, which is the smallest total possible.

Input

Multiple test cases, the number of them will be given at the very first line.

For each test case:

The first line of input will contain the integers n and k, representing the number of offices on the street (2 <= n <= 100 000) and the number of available network cables (1 <= k <= n/2).

The following n lines will each contain a single integer (0 <= s <= 1 000 000 000), representing the distance of each office from the beginning of the street. These integers will appear in sorted order from smallest to largest. No two offices will share the same location.

Output

Output should consist of a single positive integer, giving the smallest total length of network cable required to join 2k distinct offices into k pairs.

Example

Input:
1
5 2
1
3
4
6
12

Output:
4

Explanation

The sample input above represents the example scenario described earlier.

Warning: large input/output data,be careful with certain languages

Blue Mary's Note: test data has been modified on Dec. 5, 2007. All the solutions have been rejudged.

　　这题有个性质，就是你要匹配的任意两对点的连线不能重合， 否则就不是最优的了。利用这个性质去贪心解题。

 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <queue>
 #include <vector>
 using std::priority_queue;
 using std::vector;
 typedef long long LL;
 struct A{
     int l, r, pos;
        LL dis;
 };
 const int Maxn = ;
 int s[Maxn], mark[Maxn], tot;
 A l[Maxn];
 struct cmp{
     bool operator ()(A a,A b){
         return a.dis > b.dis;
     }
 };
 int main(){
 #ifndef ONl_JUDGE
     freopen ("backup.in", "r", stdin);
     freopen ("backup.out", "w", stdout);
 #endif
     int n, k;
     scanf ("%d%d", &n, &k);
     priority_queue<A, vector<A>, cmp> q;
     for (int i = ; i <= n; ++i)
         scanf ("%d", s+i);
     for(int i=;i<n;i++)
     {
         l[i].dis = s[i+]-s[i];
         l[i].pos = i;
         l[i].l = i-;
         l[i].r = i+;
     }
     l[n-].r=;
     for(int i=;i<n;i++)
         q.push(l[i]);
     LL ans = ;
     while (!q.empty()){
         A a = q.top();
         q.pop();
         if (mark[a.pos]) continue;
         ans += l[a.pos].dis;
         if (--k == ) break;
         LL w = -l[a.pos].dis;
         if (l[a.pos].l){
             w += l[l[a.pos].l].dis;
             mark[l[l[a.pos].l].pos] = ;
             l[a.pos].l = l[l[a.pos].l].l;
             if(l[a.pos].l)
                 l[l[a.pos].l].r = a.pos;
         }
         else
             mark[a.pos] = ;
         if (l[a.pos].r){
             w += l[l[a.pos].r].dis;
             mark[l[l[a.pos].r].pos] = ;
             l[a.pos].r = l[l[a.pos].r].r;
             if(l[a.pos].r)
                 l[l[a.pos].r].l = a.pos;
         }
         else
             mark[a.pos] = ;
         if (mark[a.pos] == ){
             if (l[a.pos].r) l[l[a.pos].r].l = ;
             if (l[a.pos].l) l[l[a.pos].l].r = ;
         }
         else{
             l[a.pos].dis = w;
             q.push(l[a.pos]);
         }
     }
     printf ("%lld", ans);
     return ;
 }