洛谷P3374 【模板】树状数组 1&&P3368 【模板】树状数组 2题解

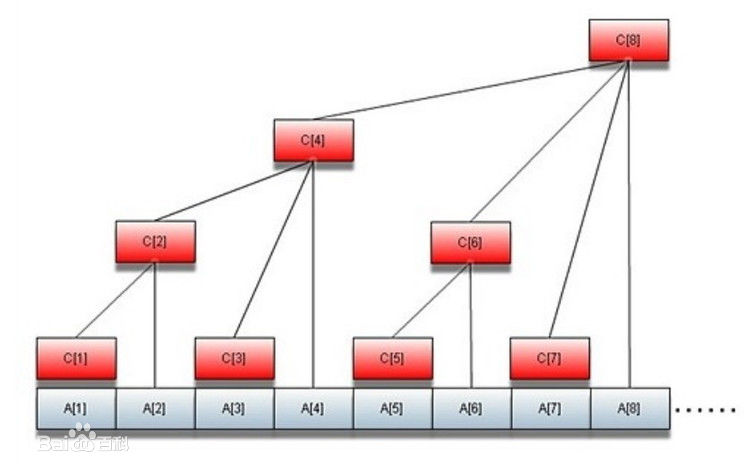
图片来自度娘~~

树状数组形如上图，是一种快速查找区间和，快速修改的一种数据结构，一个查询和修改复杂度都为log(n)，树状数组1和树状数组2都是板子题，在这里进行详解；

求和：

首先我们看一看这个图’

A数组对应各个元素的值，c数组用来求和和修改。

有连线代表着此节点的值为连线下全部子节点的和such as   c[4]=c[2]+c[3]+A[4]=A[1]+A[2]+A[3]+A[4];

貌似没有什么神仙规律。。。。。。小学找规律题都不会了嘤嘤嘤

那么我们看一下：

C1 = A1　　　　　　　　　　　　　　　　　　 对应的：1=2^0

C2 = A1 + A2　　　　　　　　　　　　　　　 　　　      2=2^1

C3 = A3　　　　　　　　　　　　　　　　　　　　　　 3=2^1+2^0

C4 = A1 + A2 + A3 + A4　　　　　　　　　　　　　　　 4=2^2

 

C5 = A5　　　　　　　　　　　　　　　　　　　　　　 5=2^2+2^0

C6 = A5 + A6　　　　　　　　　　　　　　　　　　　　6=2^2+2^1

C7 = A7　　　　　　　　　　　　　　　　　　　　　　 7=2^2+2^1+2^0

C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8　　　　　  8=2^3

那么我们按照右边的拆分，如果要询问前7个元素（前7个A的和）的和，那么我们可以把7分成如上的3个分段（区间），分别预处理这3个区间的和，把时间复杂度降到log级别的而不是分别查找7个元素并累加7次。

那么我们找到了降低时间复杂度的方法了，但是怎么实现？

换句话说怎么把一个数拆成这种区间呢？

这里我们用一个神奇的东西叫做lowbit（x）， 用来一位一位的把x拆分成以上这种形式。

我们发现，以上的形式就是一个数的二进制分解！

那么我们在将一个任意自然数表示成二进制的时候，只要每次获取这个数二进制表示的最后为值为1的一位，并每次减去它，直到这个数为0为止才算拆分完。

看着很懵？QWQ

我们还是要拿7举个栗子：

 

 7=2^2+2^1+2^0，也就是7用二进制表示为111；

那么我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数，也就是最后的1，表示长度为1的区间，获取完毕后，我们减去c[7]；现在数变为110，和ans加上c[7]

我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数，也就是第二位的1，表示长度为2的区间，获取完毕后，我们减去c[7-1]也就是c[6]；现在数变为100,和ans加上c[6]

我们获取当前数二进制表示的最后为值为1的一位以及它后面所有的0构成的数，也就是开头的1，表示长度为4的区间，获取完毕后，我们减去c[6-2]也就是c[4]；现在数为0，和ans加上c[4]

那么，我们成功把前7个数的和分解为c[7],c[7-2^0]和c[7-2^0-2^1]三个区间，对照上图，我们发现ans成功表示了前7个数（A）的和。你看一下就知道了嘛。。。QWQ

 

lowbit（x）公式就是x&(-x),

这是啥

1.我们对原数先取反，（就是在二进制表示下0变1，1变0，7（111）取反为000）

2.然后加一（000+1=001）

3.然后进行&运算（对于当前二进制数位，如果都相同（同为1或0），就返回1，else就为0）（111&001=1）

那么lowbit（7）就位1，即从右往左数数到第一个非零位的数和它后面所有的0构成的数。

概念算是讲清了，那么公式也讲一下：

对于第一步：x=~x

第二步：~x+1也就是-x，具体为什么要看电脑存储原理二进制补码，来源度娘。

第三步，与运算：x&(~x+1)也就是x&-x

至此，求和方法讲解完毕；

求和函数代码：

int query(int x){
    int ans=;
    while(x!=){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}

修改：

对于修改操作，只要查把后面元素和当前项有关的都加上修改的值就OK了，换句话说就是只要当前项能够影响到的后面的项，就都修改。

也就是把-lowbit（x）换成+lowbit（x）其余没大区别

代码：

void update(int x,int k){
    while(x<=n){//上界
        tree[x]+=k;
        x+=lowbit(x);
    }
}

然后，树状数组1差不多讲完了。。

树状数组1总代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn=;

int n,m;
int tree[maxn<<];

int lowbit(int k){
    return k&(-k);
}

void update(int x,int k){
    while(x<=n){
        tree[x]+=k;
        x+=lowbit(x);
    }
}

int query(int x){
    int ans=;
    while(x!=){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++){
        int a;
        scanf("%d",&a);
        update(i,a);
    }
    for(int i=;i<=m;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        if(a==)update(b,c);
        else printf("%d\n",query(c)-query(b-));
    }
}

接下来是树状数组2

有些不同。

 因为树状数组2变成了区间修改，单点询问，而区间修改如果用原来的方法会导致严重TLE。

那么这里我们就要用差分的方法来做这道题。

cha[i]表示a[i]-a[i-1]的值，特别的，cha[1]=a[1],因为我们设a[0]=0,那么我们，每一个数的值就可以用这个数的前缀和来表示。而这符合树状数组的求和方式。

对于区间修改，你只要修改两个值：

update(a,k);update(b+1,-k);

也就是把差分数组两边的值修改一下，区间的值就可以整体变化了。

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'')
    {
        last=ch,ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        ans=(ans<<)+(ans<<)+ch-'';
        ch=getchar();
    }
    return last=='-'?-ans:ans;
}
int n,m,c[],before=,now,judge,a,b,k;
int lowbit(int x)
{
    return x&(-x);
}
void update(int x,int y)
{
    for(;x<=n;x+=lowbit(x))c[x]+=y;
}
int sum(int x)
{
    int ans=;
    for(;x;x-=lowbit(x))ans+=c[x];
    return ans;
}
int main(){
    n=read();m=read();
    for(int i=;i<=n;i++)
    {
        now=read();
        update(i,now-before);//存入差分数组而不是原数组
        before=now;
    }
    for(int i=;i<=m;i++)
    {
        judge=read();
        if(judge==)
        {
            a=read(),b=read();k=read();
            update(a,k);update(b+,-k);//不同的操作
        }
        else
        {
            a=read();
            printf("%d\n",sum(a));
        }
    }
    return ;
}

完结撒花！