统计学习方法ｃ++实现之八 EM算法与高斯混合模型

EM算法与高斯混合模型

前言

EM算法是一种用于含有隐变量的概率模型参数的极大似然估计的迭代算法。如果给定的概率模型的变量都是可观测变量，那么给定观测数据后，就可以根据极大似然估计来求出模型的参数，比如我们假设抛硬币的正面朝上的概率为p（相当于我们假设了概率模型），然后根据n次抛硬币的结果就可以估计出p的值，这种概率模型没有隐变量，而书中的三个硬币的问题（先抛A然后根据A的结果决定继续抛B还是C），这种问题中A的结果就是隐变量，我们只有最后一个硬币的结果，其中的隐变量无法观测，所以这种无法直接根据观测数据估计概率模型的参数，这时就需要对隐变量进行估计，进而得到概率模型的参数，这里要注意，概率模型是已知的（已经假定好了），包括隐变量的模型也是假设好的，只是具体的参数未知，这时候就需要用EM算法求解未知参数，这里我用EM算法估计了高斯混合模型的参数，并用高斯混合模型实现了聚类，代码地址。

EM算法

EM算法中文名称是期望极大算法，EM是expectation maximization的缩写，从名字就可以窥视算法的核心，求期望，求极大。求谁的期望？求似然函数对隐变量的期望，所以，首先必须确定隐变量是什么。其次，对谁求极大？当然是求出概率模型的参数使得上一步的期望最大。算法如下：

输入：观测变量数据Y，隐变量数据Z（这里也是知道的？其实这里我的理解是，这里不是已知的，但是却是可以根据假设的隐变量的参数得到的），联合分布\(P(Y,Z|\theta)\), 条件分布\(P(Z|Y,\theta)\)

输出：模型参数\(\theta\)

1. E步:记\(\theta^{(i)}\)为第i次迭代参数\(\theta\)的估计值，i+1次迭代的E步， 计算

   \(Q(\theta, \theta^{(i)})=E_Z[logP(Y,Z|\theta)|Y, \theta^{(i)}]=\sum_{Z}logP(Y,Z|\theta)P(Z|Y,\theta^{(i)})\)

2. M步，求使\(Q(\theta, \theta^{(i)})\)极大的\(\theta\),作为下一次迭代的\(\theta^{(i+1)}\)

3. 重复2,3直到收敛

可以看出最重要的在于求\(Q(\theta, \theta^{(i)})\)，那么为什么每一次迭代最大化\(\sum_{Z}logP(Y,Z|\theta)P(Z|Y,\theta^{(i)})\)就能使观测数据的似然函数最大（这是我们的最终目的）？这里书上有证明，很详细，就不赘述了。先看一下我们要最大化的极大似然函数，然后这里主要引用西瓜书中的解释来从理解EM算法：

\(L(\theta)=logP(Y|\theta)=log(\sum_ZP(Y,Z|\theta))=log(\sum_ZP(Y|Z,\theta)P(Z|\theta))\)

在迭代过程中，若参数\(\theta\)已知，则可以根据训练数据推断出最优隐变量Z的值（E步）；反之，若Z的值已知，则可以方便的对参数\(\theta\)做极大似然估计(M步)。

可以看出就是一种互相计算，一起提升的过程。

这部分如果推导看不懂了，可以结合下面的二维高斯混合模型的EM算法来理解。

c++实现

这里我使用EM算法来估计高斯混合模型的参数来进行聚类，高斯混合模型还有一个很大的作用是进行前景提取，这里仅仅用二维混合高斯模型进行聚类。

代码结构

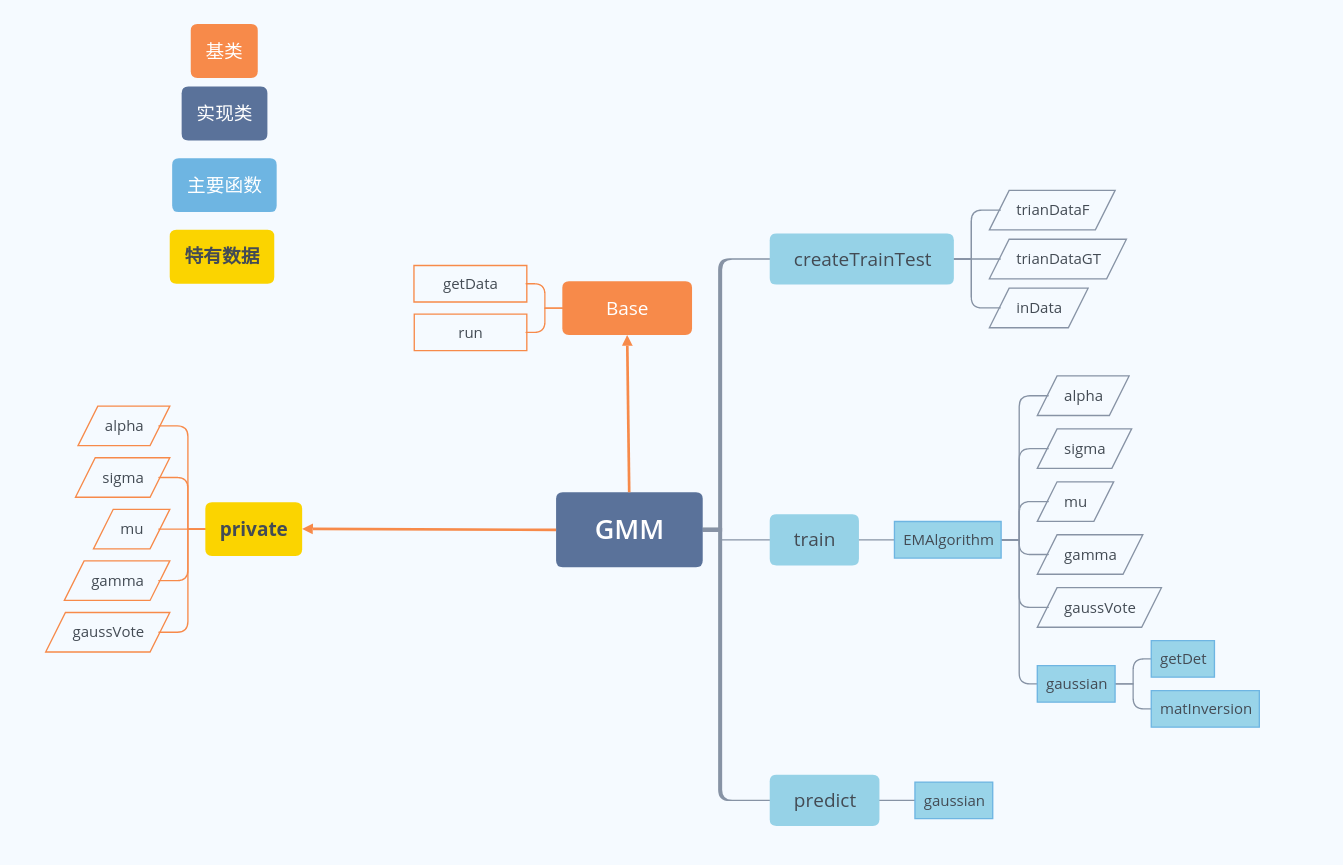
关键代码

这里实现起来其实没什么难点，难点在于推导参数的更新公式，详情参考西瓜书p206。

void GMM::EMAlgorithm(vector<double> &alphaOld, vector<vector<vector<double>>> &sigmaOld,
        vector<vector<double>> &muOld) {
// compute gamma
    for (int i = 0; i < trainDataF.size(); ++i) {
        double probSum = 0;
        for (int l = 0; l < alpha.size(); ++l) {
            double gas = gaussian(muOld[l], sigmaOld[l], trainDataF[i]);
            probSum += alphaOld[l] * gas;
        }
        for (int k = 0; k < alpha.size(); ++k) {
            double gas = gaussian(muOld[k], sigmaOld[k], trainDataF[i]);
            gamma[i][k] = alphaOld[k] * gas / probSum;
        }
    }
// update mu, sigma, alpha
    for (int k = 0; k < alpha.size(); ++k) {
        vector<double> muNew;
        vector<vector<double>> sigmaNew;
        double alphaNew;
        vector<double> muNumerator;
        double sumGamma = 0.0;
        for (int i = 0; i < trainDataF.size(); ++i) {
            sumGamma += gamma[i][k];
            if (i==0) {
                muNumerator = gamma[i][k] * trainDataF[i];
            }
            else {
                muNumerator = muNumerator + gamma[i][k] * trainDataF[i];
            }
        }
        muNew = muNumerator / sumGamma;
        for (int i = 0; i < trainDataF.size(); ++i) {
            if (i==0) {
                auto temp1 = gamma[i][k]/ sumGamma * (trainDataF[i] - muNew);
                auto temp2 = trainDataF[i] - muNew;
                sigmaNew = vecMulVecToMat(temp1, temp2);
            }
            else {
                auto temp1 = gamma[i][k] / sumGamma * (trainDataF[i] - muNew);
                auto temp2 = trainDataF[i] - muNew;
                sigmaNew = sigmaNew + vecMulVecToMat(temp1, temp2);
            }
        }
        alphaNew = sumGamma / trainDataF.size();
        mu[k] = muNew;
        sigma[k] = sigmaNew;
        alpha[k] = alphaNew;
    }
}

总结

前面的代码一直用vector来实现向量，但是这里用到了矩阵，矩阵的相关计算都添加的计算函数。最正规的应该是写个类，实现矩阵运算，但是这里偷懒了，以后写代码一定要考虑周到，这样添添补补的太低效了。