[Python3 练习] 006 汉诺塔2 非递归解法
题目:汉诺塔 II
- 接上一篇 [Python3 练习] 005 汉诺塔1 递归解法
- 这次不使用递归
- 不限定层数
(1) 解决方式
- 利用“二进制”
(2) 具体说明
- 统一起见
- 我把左、中、右三根柱子依次称为 A 塔、B 塔、C 塔
- 金片默认都在 A 塔
- n 片金片从小到大依次编号为 0 号、1 号、……、n-1 号
1) 举个“栗子”
- 假设有一个 4 层高的汉诺塔,设初始值为 0000(2)
- 按 "8"、"4"、"2"、"1" 称呼二进制的各位
- "8"位、"4"位、"2"位、"1"位依次对应 3 号金片、2 号金片、1号金片、0 号金片
- 如图
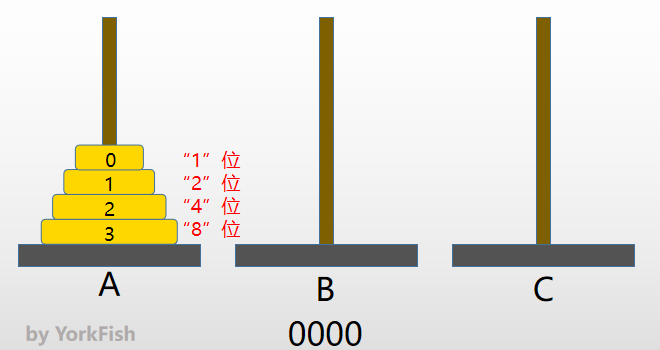
- 开始累加,每次加 1
- 0000(2) -> 0001(2)
- "1"位由 0 变 1,则将 0 号金片右移,即将 0 号金片由 A 塔移至 B塔
- 补充:若要将 C 塔上的金片右移,则移至 A 塔,三个塔是循环的
- 如图
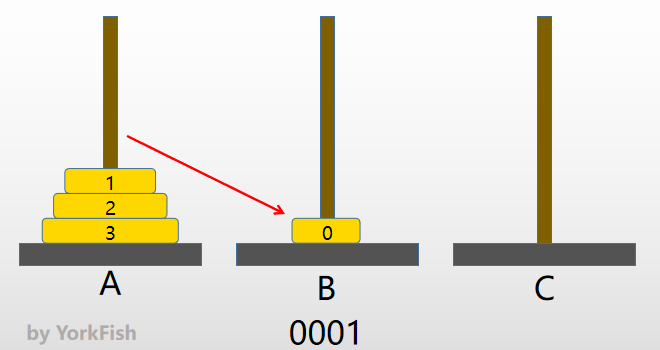
- 0001(2) -> 0010(2)
- 产生进位;进到哪位,则移动该位对应的金片
- 此时进位至"2"位,则右移 1 号金片
- 右移 1 号金片时,因为 1 号金片不能放在 B 塔的 0 号金片上方,所以继续向右走,C 塔正好符合要求
- 如图
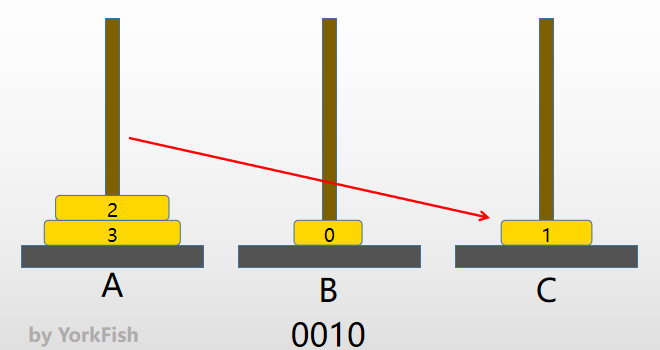
- 0010(2) -> 0011(2)
- "1"位由 0 变 1,则将 B 塔的 0 号金片右移至 C 塔
- 如图
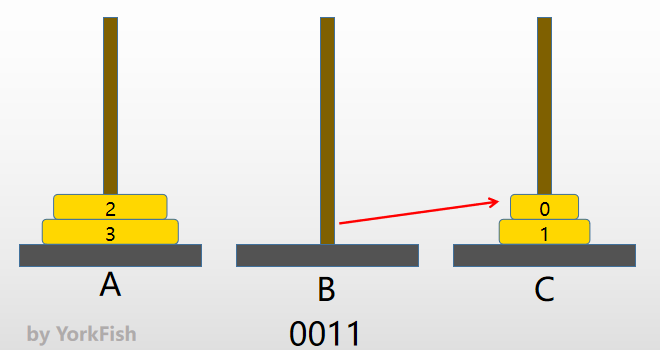
- 0011(2) -> 0100(2)
- 产生进位,此时进至“4”位,则将 A 塔上的 2 号金片右移至 B 塔
- 如图

- 0100(2) -> 0101(2)
- 个位由 0 变 1,则将 C 塔的 0 号金片右移至 A 塔
- 如图
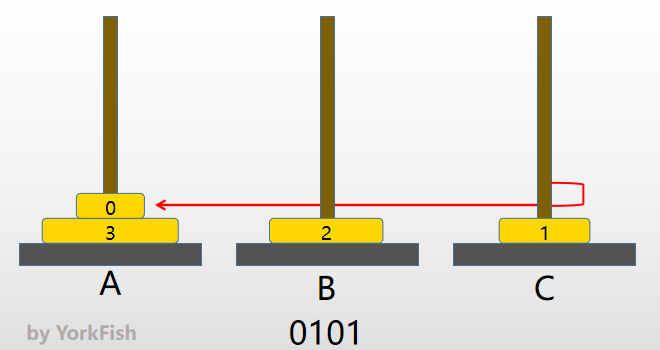
……
- 按这个方法进行下去,当数字变成 "1111" 时,A 塔的 4 片金片就都在 C 塔上了
2) 一些说明
此“二进制”方法可以解决汉诺塔,但奇数金片与偶数金片在结果上有些许不同
- 按照上面的规则,奇数金片最终会移至 B 塔,偶数金片最终会移至 C 塔
- 可借高数中“轮换对称性”的思想,在面对奇数金片时,把原来的 B 塔看成 C 塔,把原来的 C 塔看成 B 塔
上面的操作有 2 个规律
- 规律一
- 因为每走一步,数值加 1,所以该二进制数即为步数
- 该二进制数末尾 0 的个数对应要移动的金片编号
- 没有 0,即为 0 个 0,对应 0 号金片;可回顾图 "0001"、"0011"、"0101"
- 1 个 0,对应 1 号金片;可回顾图 "0010"
- 2 个 0,对应 2 号金片;可回顾图 "0100"
- 依此类推
- 规律二
- 编号为 0、2、4……的金片,总是进行右移操作
- 编号为 1、3、5……的金片,总是进行左移操作
- 三根柱子,右移 2 格即为左移 1 格
- 规律一
3) 计算移动次数
- 按递归的思路,汉诺塔可分成三大步
- 将 A 塔的上面 n-1 片金片移至 B 塔
- 将 A 塔剩余的 1 片金片移至 C 塔
- 将 B 塔的 n-1 片金片移至 C 塔
- 设 f(n) 为 n 片金片完成移动需要的最少次数,则 f(n) = f(n-1) + 1 + f(n-1),即 f(n) = 2f(n-1) + 1
- 若只有 1 片金片,则 f(1) = 1
- 若有 2 片金片,则 f(2) = 3
- 若有 3 片金片,则 f(3) = 7
- 照此规律,可假设 f(n) = 2n - 1
- 莫名想到线代中用的“第一类数学归纳法”,我献丑证一下,算是温故知新
- 证明 f(n) = 2n - 1 成立:
- 当 n = 1 时,f(1) = 21 - 1 = 1,成立
- 当 n = k 时,设 f(k) = 2k - 1 成立
- => 当 n = k + 1 时,f(k+1) = 2f(k) + 1 = 2 * (2k - 1) + 1 = 2k+1 - 1,满足假设
- => 汉诺塔的移动次数为 f(n) = 2n - 1,证毕
(3) 程序
1) 代码
# 不使用递归
def hanoi(n):
tower_belong = [0] * n # 用列表开辟 n 个空间,用于存放 n 个金片各自的编号,编号对应塔号
# 金片移动,编号对应更改
if n % 2 == 0: # 金片数量不同,塔的排序不同
tower_name = ['A', 'B', 'C'] # 若 n 为偶数,最终所有金片恰好能移到右塔
else:
tower_name = ['A', 'C', 'B'] # 若 n 为奇数,最终所有金片会移到中塔
# 用“轮换对称”将 B、C 两塔互换名字,以实现“负负得正”
for step in range(1, 2**n): # n 片金片最少需要移动 2^n - 1 次
bin_step = bin(step) # 求得 step 的二进制数值
gold_num = len(bin_step) - bin_step.rfind('1') - 1
# 计算 step 末尾 0 的个数,得到金片编号;上面说的“规律一”
# 如 step = 0b0001,则 step 末尾 0 的个数为 0,表示此刻应移动 0 号金片
# 如 step = 0b0100,则 step 末尾 0 的个数为 2,表示此刻应移动 2 号金片,依此类推
# rfind 是从 0 开始计数,所以再减个 1
print(f"第 {step:2} 步:移动 {str(gold_num)} 号金片,从 {tower_name[tower_belong[gold_num]]} 塔到", end=' ') # 移出金片的塔
if gold_num % 2 == 0: # 若 num 为 偶数,则右移
tower_belong[gold_num] = (tower_belong[gold_num] + 1) % 3
# 若从 C 塔右移,则又回到了 A 塔
else: # 若 num 为奇数,则左移
tower_belong[gold_num] = (tower_belong[gold_num] + 2) % 3
# 若从 A 塔左移,则又去到了 C 塔
print(tower_name[tower_belong[gold_num]], '塔') # 移入金片的塔
# 清爽、无注释版
def hanoi(n):
tower_belong = [0] * n
if n % 2 == 0:
tower_name = ['A', 'B', 'C']
else:
tower_name = ['A', 'C', 'B']
for step in range(1, 2**n):
bin_step = bin(step)
gold_num = len(bin_step) - bin_step.rfind('1') - 1
print(f"第 {step:2} 步:移动 {str(gold_num)} 号金片,从 {tower_name[tower_belong[gold_num]]} 塔到", end=' ')
if gold_num % 2 == 0:
tower_belong[gold_num] = (tower_belong[gold_num] + 1) % 3
else:
tower_belong[gold_num] = (tower_belong[gold_num] + 2) % 3
print(tower_name[tower_belong[gold_num]], '塔')
2) 运行情况
- 3 层汉诺塔

- 4 层汉诺塔
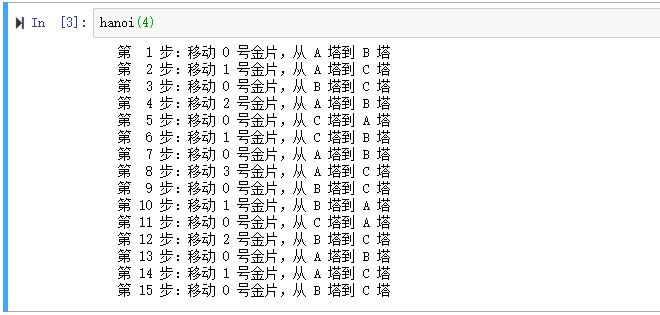
[Python3 练习] 006 汉诺塔2 非递归解法的更多相关文章
- PTA 汉诺塔的非递归实现(C 语言)
借助堆栈以非递归(循环)方式求解汉诺塔的问题(n, a, b, c), 即将N个盘子从起始柱(标记为“a”)通过借助柱(标记为“b”)移动到目标柱(标记为“c”), 并保证每个移动符合汉诺塔问题的要求 ...
- C#中汉诺塔问题的递归解法
百度测试部2015年10月份的面试题之——汉诺塔. 汉诺塔就是将一摞盘子从一个塔转移到另一个塔的游戏,中间有一个用来过度盘子的辅助塔. 百度百科在此. 游戏试玩在此. 用递归的思想解决汉诺塔问题就是分 ...
- [Python3 练习] 005 汉诺塔1 递归解法
题目:汉诺塔 I (1) 描述 传说,在世界中心贝拿勒斯(在印度北部)的圣庙外有左中右三根足够长的柱子(塔) 左边柱子上套着 64 片金片,金片按"上小下大"排,其余两根是空柱子 ...
- 汉诺塔算法的递归与非递归的C以及C++源代码
汉诺塔(又称河内塔)问题其实是印度的一个古老的传说. 开天辟地的神勃拉玛(和中国的盘古差不多的神吧)在一个庙里留下了三根金刚石的棒,第一根上面套着64个圆的金片,最大的一个在底下,其余一个比一 个小, ...
- python汉诺塔问题的递归理解
一.问题背景 汉诺塔问题是源于印度一个古老传说. 源于印度一个古老传说的益智玩具.大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘.大梵天命令婆罗门把圆盘从下 ...
- 理解 Hanoi 汉诺塔非递归算法
汉诺塔介绍: 汉诺塔(港台:河内塔)是根据一个传说形成的数学问题: 最早发明这个问题的人是法国数学家爱德华·卢卡斯. 传说越南河内某间寺院有三根银棒,上串 64 个金盘.寺院里的僧侣依照一个古老的预言 ...
- 汉诺塔算法c++源代码(递归与非递归)[转]
算法介绍: 其实算法非常简单,当盘子的个数为n时,移动的次数应等于2^n - 1(有兴趣的可以自己证明试试看).后来一位美国学者发现一种出人意料的简单方法,只要轮流进行两步操作就可以了.首先把三根柱 ...
- c++迭代递归实现汉诺塔(5种迭代方法满足你)
#include <iostream> //从A到C using namespace std; int n; void ready() { cout << "请输入汉 ...
- 汉诺塔问题C++实现
大家好,我是小鸭酱,博客地址为:http://www.cnblogs.com/xiaoyajiang 以下进行汉诺塔问题的递归实现 #include <iostream.h> int gb ...
随机推荐
- ssh跳板到其他服务器
https://my.oschina.net/foreverich/blog/657075 http://mingxinglai.com/cn/2015/07/ssh-proxycommand/ 查看 ...
- pymysql基本操作
https://www.cnblogs.com/woider/p/5926744.html https://www.runoob.com/python3/python3-mysql.html 注意: ...
- dd命令注意:dd:unrecognized operand 'if'
如果是 idd if=boot.bin 在等号两边不要有空格
- 双层for循环用java中的stream流来实现
//双重for循环for (int i = 0; i < fusRecomConfigDOList.size(); i++) { for (int j = 0; j < fusRecomC ...
- asp.net能否上传文件夹下所有文件
HTML部分 <%@PageLanguage="C#"AutoEventWireup="true"CodeBehind="index.aspx. ...
- Form 表单用 Ajax 提交数据并用 jQuery Validate 验证
表单填写需要验证可用插件 jQuery Validate 提交数据使用 Ajax 可操控性得到提到 注意:请自行引入 jQuery 和 jQuery Validate HTML 代码 <form ...
- SetwindowText 之线程阻塞
示意代码: CriticalSection g_Section; CDialog g_Dlg; // 工作线程函数UINT TreadFunc_A(PVOID para){ Sleep(10); g_ ...
- #1112-JSP生命周期
JSP 生命周期 理解JSP底层功能的关键就是去理解它们所遵守的生命周期. JSP生命周期就是从创建到销毁的整个过程,类似于servlet生命周期,区别在于JSP生命周期还包括将JSP文件编译成ser ...
- [springboot jpa] [bug] Could not open JPA EntityManager for transaction
前言 最近,测试环境遇到了一个问题.经过一番百度加谷歌,终于解决了这个问题.写下这篇博客是为了记录下解决过程,以便以后查看.也希望可以帮助更多的人. 环境 java版本:8 框架:spring clo ...
- Day3 01 枚举
枚举:关键字 enum 主要为了限定了选择范围,声明了一组相关的值类型的集合. 1.枚举类型,实质上是整整 2.如果不进行赋值操作,枚举类型从0开始递增. 3.枚举不能定义字段 属性 方法. 例如 ...
