牛客练习赛46 E 华华和奕奕学物理 （树状数组）

https://ac.nowcoder.com/acm/contest/894/E

一开始写了一个简单的模拟 通过率只有5%......

看题解真的理解了好久！！肥宅大哭orz

题解如下

最后一句：“维护6个树状数组即可”.....喵喵喵？？

先学一下树状数组吧：

链接在这
https://blog.csdn.net/Small_Orange_glory/article/details/81290634

结合代码讲比较容易理解

#include<bits/stdc++.h>
using namespace std;
const int maxn=4e6+;
const int T=3e5+;
const int mod=1e9+;
const int g=;
#define ll long long
ll bit[][maxn];
void add(ll b[],int i,ll C)  //更新树状数组
{
    while(i<maxn)
    {
        b[i]=(b[i]+C)%mod;
        i+=i&-i;
    }
}
ll sum(ll b[],int i)   //求和 前i个元素的和
{
    ll  ans=;
    while(i>)
    {
        ans+=b[i];
        i-=i&-i;
    }
    return ans%mod;
}
int main()
{
    int Q;scanf("%d",&Q);
    while(Q--)
    {
        int op,v,t,m;scanf("%d%d%d",&op,&v,&t);
        if(op==)
        {
            int V=v+g*(T-t);
            scanf("%d",&m);
            add(bit[],V,1LL*m*v%mod*v%mod);
            add(bit[],V,1LL*m*g*g%mod);
            add(bit[],V,1LL*m*g*g%mod*t%mod*t%mod);
            add(bit[],V,1LL**m*g*g%mod*t%mod);
            add(bit[],V,1LL**m*v%mod*g%mod);
            add(bit[],V,1LL**m*v%mod*g*t%mod);
        }
        else
        {
            int V=min(v+g*(T-t),maxn-);
            ll ans=;
            ans+=sum(bit[],V);
            ans+=sum(bit[],V)*t%mod*t%mod;
            ans+=sum(bit[],V);
            ans-=sum(bit[],V)*t%mod;
            ans+=sum(bit[],V)*t%mod;
            ans-=sum(bit[],V);
            ans%=mod;
            if(ans<)
                ans+=mod;
            printf("%lld\n",ans);
        }
    }
    return ;
}

先讲为什么维护6个数组：

因为将公式

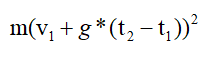
拆开就会变成含有6项的多项式：

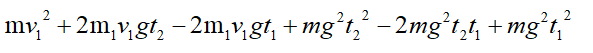
我们将符合条件的小球的分别记录到6个数组中 这样方便求和

那么什么是符合条件的小球呢？

仔细看题解里说：

若某一时刻a球比b球速度快，则a球始终比b球速度快。

所以如果末尾时间a球比b球快 那么a球始终比b球快

所以判断某一时刻速度比v小的小球有哪些 假设在这一时刻扔下一个初速度为v的小球 只需要看哪些小球在最后的时刻速度比这个初速度为v的小球速度慢就好了

那么对于每一次op==1 我们就更新一次数组 把v+g*(T-t)之后的树状数组全部更新

对于每一次op==2 我们就把前v+g*(T-t)项求和

照着模拟几遍就理解了（而我想了一晚上）