岭回归、lasso

参考：https://blog.csdn.net/Byron309/article/details/77716127     ----    https://blog.csdn.net/xbinworld/article/details/44276389

参考：https://blog.csdn.net/bitcarmanlee/article/details/51589143

1、首先介绍线性回归模型（多元）原理，模型可以表示为：

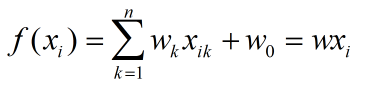
损失函数可以表示为：

这里的 1/2m 主要还是出于方便计算的考虑，在求解最小二乘的时并不考虑在内；

最小二乘法可得到最优解：

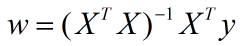
监督学习有2大基本策略，经验风险最小化和结构风险最小化；

经验风险最小化策略为求解最优化问题，线性回归中的求解损失函数最小化问题即经验风险最小化，经验风险最小化定义：

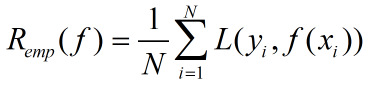
求解最优化问题可以转化为：

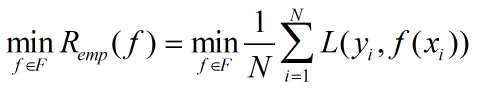
结构化风险最小化是为了防止过拟合现象提出的策略；结构风险最小化等价于正则化，在经验风险上加上表示模型复杂度的正则化项，定义如下：

这里讨论的岭回归和Lasso，也就是结构风险最小化的思想，在线性回归的基础上，加上模型复杂度的约束。

其中几种范数（norm）的定义如下：

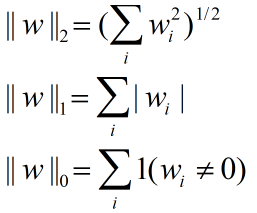
岭回归的损失函数表示：

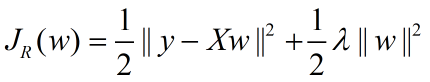
观察这条式子很容易的可以联想到正则化项为L2范数，也即L2范数+损失函数其实也可以称为岭回归；

最小二乘求解参数：

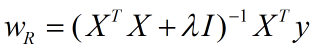
Lasso的损失函数表示：

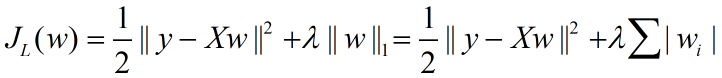
由于Lasso损失函数的导数在0点不可导，因此不能直接利用梯度下降求解；引入subgradient的概念，考虑简单函数，即x只有1维的情况下，即简单函数表示：

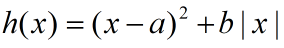
首先定义|x|在0点的梯度，即subgradient，

函数在某一点的导数可以看成函数在这一点上的切线。那么在原点，可以在实线下方找到无数条切线，形成曲线族；我们把这些切线斜率的范围定义为这点的subgradient；也即|x|在0点的导数是在-1到1范围内的任意值；

所以可以得到h(x)的导数：

在x=0的时候，按照上面的subgradient可以得到，x=0时斜率的区间在x>0和x<0之间；当-b<2a<b时，在x=0时，f^'(x)能取到值0；也就是f(x)到达极值点，这也可以解释lasso下的解会稀疏的原因：在b的取值在一定范围内时，只要x为0，f^'(x)就恒为0； （这句话本人不是特别理解）（先存疑），

有关subgradient的解释：https://blog.csdn.net/lansatiankongxxc/article/details/46386341

当x拓展到多维向量时，导数方向的变化范围更大，问题更为复杂；常见解决方法如下：

1、贪心算法；每次先找到与目标最相关的feature，固定其他系数，优化这个feature的系数，具体求导也用到subgradient；代表算法有LARS，feature-sign search等；

2、逐一优化；每次固定其他的维度，选择一个维度进行优化；因为只有一个方向有变化，所以转化为简单的subgradient问题，反复迭代所有维度，达到收敛；代表算法有coordinate descent，block coordinate descent等；

Lasso和ridge的几何意义如下图：

红色椭圆和蓝色的区域的切点就是目标函数的最优解；可以看到，如果是圆，很容易切到圆周的任意一点，但是很难切到坐标轴上。则在该纬度上取值不为0，因此没有系数；如果是菱形或多边形，则很容易切到坐标轴上，使部分维度特征权重为0，因此很容易产生稀疏的结果；