【算法】Tarjan

参考资料：

图论相关概念 - OI WIKI | 强连通分量 - OI WIKI

初探tarjan算法 | Tarjan，你真的了解吗

一、概念

• 子图：

对一张图 \(G=(V,E)\)，若存在另一张图 \(H=(V',E')\) 满足 \(V'\subseteq V\) 且 \(E'\subseteq E\)，则称 \(H\) 是 \(G\) 的 子图 (subgraph)，记作 \(H \subseteq G\)。——OI WIKI

通俗点说就是如果你能在图 G 中找到一部分和 H 一样，那么 H 就是 G 的子图。

或者这样理解，图 H 里面的所有边都能在 G 里面找到，那么就是子图了。

• 连通和可达

现在有两个点 x 和 y，如果在图 G 里能找到一条从 x 走到 y 的路径，那么就称之为 x 可达 y。如果图 G 是无向图的话，还可以说 x 与 y 连通。

现有三个定义：

1. 如果无向图 G 里面任意两点都互相连通，那么图 G 就是连通图。

2. 如果有向图 G 里面任意两点都互相可达，那么图 G 就是强连通的。

3. 如果有向图 G 里面的有向边全部都为无向边后，任意两点都互相连通，那么图 G 就是弱连通的。

• （强/弱）连通分量

这是上一条的补充，也是这讲里面几乎是最重要的一个概念。

如果在无向图 G 中可以找到一个最大的连通子图 H，那么 H 就是 G 的连通分量

类似的，我们可以将连通分量的定义推广到强连通分量和弱连通分量上

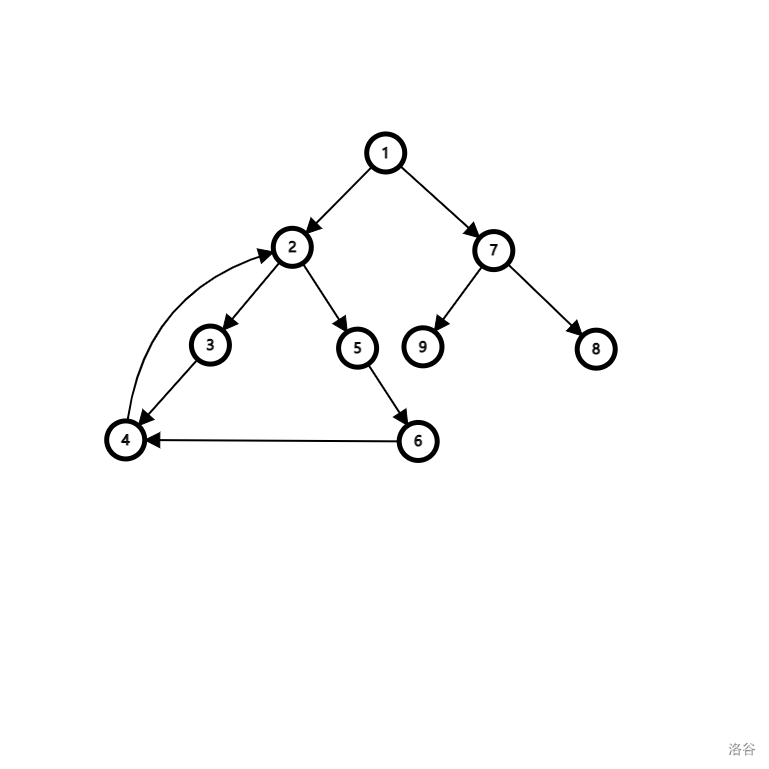
\(\tiny\text{图 1-1}\)

如上图 G，节点 2 3 4 构成的图不是 G 的强连通分量（不是最大的），但是节点 2 3 4 5 6 构成的图是 G 的强连通分量。当然点 1，7，8，9都分别是一个强连通分量

更通俗一点的，强连通分量可以理解为在有向图中找一个最大的环。

• Tarjan

Tarjan是一种快速求出有向图里面强联通分量的算法。

现在，我们将有向有环图抽象成 DFS 树，那么除了树边还会有其它边，比如下图：

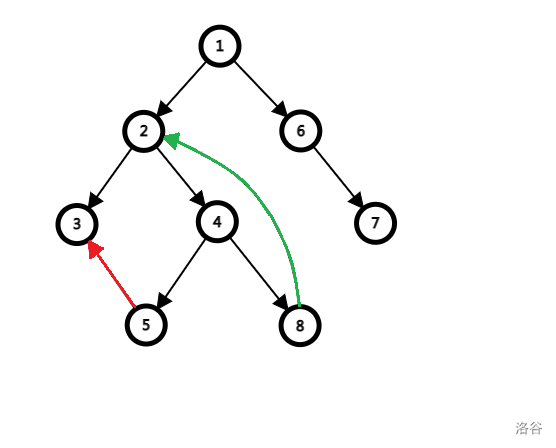
\(\tiny\text{图 1-2}\)

其中黑边为树边，红边和绿边为非树边。

特别的，我们规定红边为横插边，也就是非树边的两端没有父子关系；绿边为返祖边，也就是非树边的两端有父子关系。

但是，非树边的两端是节点 8 和节点 7 是不可能的，如果这样的话，当访问到节点 8 时为继续搜索节点 7 ，与现在这颗 DFS 树不符。

不难发现，绿边可以构成一个环，而红边不行。

而 Tarjan 算法一般用于缩点，也就是将一个强连通分量看做一个点，对结果并不影响。

二、实现

依旧要运用上面的 DFS 搜索树来实现 Tarjan

于是我们有了以下变量：

   dfn[i] 表示 i 的 dfs 序
   dn 表示 dfs 序数

当然还有链式前项星的那些变量。

判断两个点 u,v 强连通的条件：\(u\) 可达 \(v\)，且 \(v\) 可达 \(u\)。

虽然听起来像废话，但我们可以从这个条件入手思考 Tarjan。

既然 \(u\) 要可达 \(v\) 的话，我们就直接遍历 \(u\) 所有可达的节点。

—— 于是

• 第一步：遍历 u

void tarjan(int x){
	dfn[x]=++dn;//更新 dfn 数组
	for(int i=head[x];i;i=edge[i].nex){
		int nex=edge[i].to;
		if(dfn[nex]==0){//如果之前没有被访问到
			tarjan(nex);//访问
		}
	}
    //当然这里会有一个判断 u 是否可构成强连通分量的语句，但现在不急
}

然后考虑什么时候 \(v\) 可达 \(u\)。

不难发现，当 \(v\) 有一条指向 \(u\) 或者 \(u\) 的祖先的时候，\(v\) 一定可达 \(u\)。

并且，一个节点只能在一个强连通分量里面，不妨用反证法证明一下，如果一个节点同时在两个强连通分量里面，那么这两个互相强连通的分量合在一起也是强连通的，并且比之前的分量大，与之前假设的不相符。

Q：怎么判断 \(u\) 节点是该强联通分量最先访问的节点呢？

再开一个数组存贮 \(low_{[u]}\) 表示 \(u\) 节点及 \(u\) 的子节点中的 \(dfn\) 最小值。

这样当 \(low_{[u]}=dfn_{[u]}\) 时就表示点 \(u\) 是最先访问的节点了。

——所以

• 第二步：更新 \(low\) 数组

void tarjan(int x){
	low[x]=dfn[x]=++dn;//目前dfs序的最小值就是x的dfs序
	stk[++top]=x;//入栈
	inst[x]=true;
	for(int i=head[x];i;i=edge[i].nex){
		int nex=edge[i].to;
		if(dfn[nex]==0){//如果子节点还没被访问过/还没入过栈
			tarjan(nex);//先将它的子节点遍历，更新nex的low值
			low[x]=min(low[x],low[nex]);//nex可能会连到x的祖先，所以进行更新的是low值
		}
		else if(inst[nex]==true){//之前就访问过了，说明它的dfs序比x要小
			low[x]=min(low[x],dfn[nex]);//所以进行更新的是dfn值
		}
		/*
		if(inst[nex]==false){
			那么nex一定不属于u的强联通分量，直接continue
		}
		*/
	}
}

Q：怎么确保 \(v\) 贡献给 \(u\) 的节点一定可以和 \(u\) 构成强连通分量呢？

考虑维护一个栈，记录 \(u\) 之后可以和它构成强连通分量的点。也就是说，每当遍历到一个点时，先判断一下它有没有已经属于一个强连通分量了，如果已经属于，那么就直接弹出栈。

由于不属于 \(u\) 强联通分量的点都已经被弹出栈了，所以当前在 \(u\) 之后入栈的元素都一定属于它的强联通分量。

——最后一步！

• 第三步：弹栈

inline void tarjan(int x){
	/*前两步代码
	low[x]=dfn[x]=++dn;
	stk[++top]=x;
	inst[x]=true;
	for(int i=head[x];i;i=edge[i].nex){
		int nex=edge[i].to;
		if(dfn[nex]==0){
			tarjan(nex);
			low[x]=min(low[x],low[nex]);
		}
		else if(inst[nex]==true){
			low[x]=min(low[x],dfn[nex]);
		}
	}
	*/
	if(dfn[x]==low[x]){//是当前强联通分量中最先访问的节点
		cn++;//染色操作
		while(stk[top]!=x){//在其后的都要弹出
			int now=stk[top--];
			inst[now]=false;
			col[now]=cn;
		}
		int now=stk[top--];//自己也要弹出
		inst[now]=false;
		col[now]=cn;
	}
}

三、时间复杂度

\(O(n)\)，结束。