APIO刷题

APIO2010

APIO2010T1 特别行动队

记 \(dp[i]\) 表示划分前 \(i\) 个时的答案，则有 \(dp[i] = max\{ dp[j] + a(sum[i]-sum[j])^2+b(sum[i]-sum[j])+c\ | 0\le j< i\}\)

若 \(p<q\) ，且满足 \(2a\times sum[i]\times (sum[q]-sum[p])<=(a\times sum[q]^2-b\times sum[q]+dp[q])-(a\times sum[p]^2-b\times sum[p]+dp[p])\) ，则由于 \(a<-1 且 sum[i]<sum[i+1]\) ，所以 \(LHS\) 变小，\(p\) 一定不会比 \(q\) 优，弹出队列。

时间复杂度：\(O(n)\)

APIO2010T2 巡逻

对于一棵树，每条边一定走 \(2\) 遍。

当 \(k=1\) ：我们发现把树的直径给连成环以后，减少的贡献最大，答案最小。

当 \(k=2\) ：无非找两次直径连成环，但这环可能会重叠，怎么办？

有一个很方便的做法，就是第一次跑完直径后，给直径上的所有边权乘以 \(-1\) ，再跑一次直径。

原理很简单，\(1+(-1)=0\) 。

时间复杂度：\(O(n)\)

APIO2010T3 信号覆盖

题目即求：\(\frac{每种方案被圆覆盖（含边界）的点数}{C_n^3}\)

由于每种方案的三个点必定被覆盖，所以可以变成 \(\frac{每种方案在圆内的点数}{C_n^3}+3\)

转换视角，分子即为无序四元组 \((i,j,k,t)\) 满足 \(t\) 在 \(i,j,k\) 构成的圆内的对数。

题目保证三点不共线，四点不共圆，那么无非就两种情况：四个点形成凹四边形/凸四边形。



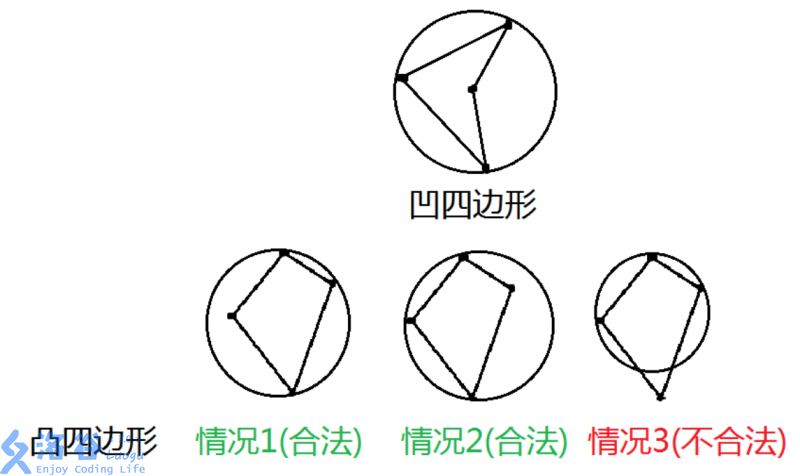
凹四边形的贡献为 \(1\) ，凸四边形的贡献为 \(2\) （凸多边形的其中一对角和 \(>180°\)）

设凹四边形有 \(k\) 个，那么凸四边形有 \(C_n^4-k\) 个，答案为 \(\frac{k+2(C_n^4-k)}{C_n^3}+3\)

瓶颈在于如何求出凹四边形数目，假设凹点为 \(D\) ，那么我们要找出三角形 \(ABC\) 包括 \(D\) 。

正难则反，考虑不包括 \(D\) 。

以 \(D\) 为坐标原点，所有点极角排序，然后用尺取法计算得到第 \(i\)个点最远到第 \(j\) 个点，使两向量夹角 \(<180°\) ，那么在 \((i,j)\) 任意选一个 \(k\) 构成的三角形均不包括 \(D\) 。

数点完拿 \((C_{n-1}^3 - 答案)\) ，即为所有包括 \(D\) 的三角形数了。

时间复杂度：\(O(n^2logn)\)

APIO2012

APIO2012T1 派遣

枚举所有的领导者，在它子树内贪心挑薪水小的人，这样暴力是 \(O(n^2)\) 的。

用 左偏树 优化一下即可，挺裸的。

时间复杂度：\(O(nlogn)\)

APIO2013

APIO2013T3 出题人

\(1.in-6.in\) 全是卡单源最短路，\(7.in-8.in\) 是神秘程序。

神秘问题：给一张图的每个节点染色，使得任何一条边两端点颜色不同，求最少用多少种不同的颜色

• 1: ModifiedDijkstra.cpp & FloydWarshall.cpp

卡掉 \(Floyd\) ，直接 \(V=101\) ，无边，\(1\) 组询问即可。

使用次数：\(105,T=107\)

• 2: FloydWarshall.cpp & OptimizedBellmanFord.cpp

卡掉 \(BellmanFord\) ，不卡 \(Floyd\) ，那么我们令 \(V=100\) ，这样 \(Floyd\) 不会超时。

然后，构造一些 \(j\) 到 \(i\) 边权依次增加 (\(i<j\)) 即可，让 \(BellmanFord\) 跑满 \(V-1\) 次。

使用次数：\(2190,T=2222\)

• 3: OptimizedBellmanFord.cpp & FloydWarshall.cpp

卡掉 \(Floyd\) ，不卡 \(BellmanFord\) ，那么我们令 \(V=101\) ，无边权，\(1\) 组询问即可。

使用次数：\(105,T=105\) ，卡的真紧...

• 4: FloydWarshall.cpp & ModifiedDijkstra.cpp

卡掉堆优化的\(dijkstra\) ，我们可以造负权图。



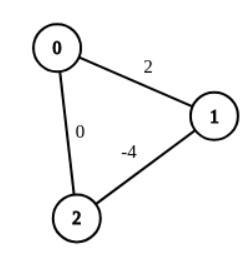
我们构造一连串负团（见上图），边权依次倍增，它复杂度就被卡成指数级了。

使用次数：\(151,T=157\)

• 5: ModifiedDijkstra.cpp & OptimizedBellmanFord.cpp

卡掉 \(BellmanFord\) ，不卡 \(dijkstra\) ，那简单了。

我想办法把 \(BellmanFord\) 的优化给抵消掉，那我建自环卡飞不就得了？

所以令 \(V=300\) ，然后 \(0\) 连向 \(1\) ，边权随意，然后对于 \(i\ge 2\) 建一个负自环，再随机加点边。

查询查 \(10\) 次 \(0\) 到 \(1\) 。

使用次数：\(1016,T=1016\)

• 6: OptimizedBellmanFord.cpp & ModifiedDijkstra.cpp

卡掉 \(dijkstra\) ，不卡 \(BellmanFord\) ，这和 #4 类似。

疯狂调参卡常即可。

使用次数：\(143,T=143\)

• 7: Gamble1.cpp & RecursiveBacktracking.cpp

这个Gamble1.cpp是恒过器，所以我们只需要使RecursiveBacktracking.cpp超时即可。

它是个爆搜，所以……我随便造一组大数据就把它卡飞？？

使用次数：\(3004,T=3004\)

• 8: RecursiveBacktracking.cpp & Gamble2.cpp

这个Gamble2.cpp是恒挂器，所以我们只需要使RecursiveBacktracking.cpp跑的出来。

采用黑白染色，然后随便找黑点和白点连边即可，但 \(i\) 和 \(i+1\) 必须连。

使用次数：\(3004,T=3004\)

[汇总] 所有的数据生成器：代码

答案

APIO2019

预计得分：\(100+100+80=280\)

APIO2019T1 奇怪装置

数学题，求个线段交即可。

时间复杂度：\(O(nlogn)\)

APIO2019T2 桥梁

将操作分块，然后用带撤销并查集维护一下即可。

设块长为 \(S\) ，则复杂度为 \(O(Sqlog(n)+\frac{qmlog(m)}{S})\)

在 \(S=\sqrt{m}\) 左右时复杂度最优，为 \(O(q\sqrt{m} logm)\)

UPD: 在洛谷上被硬生生卡常了,完美GG

其实可以再优化（其实是因为洛谷老爷机太慢），把排序用归并实现，块长为 \(\sqrt{\frac{m}{log(n)}}\)，可达到 \(O(q\sqrt{mlogm})\)

时间复杂度：\(O(q\sqrt{mlogm})\)

APIO2019T3 路灯

假设 \(i\) 所能到达的最左和最右的位置为 \(l_i\) 和 \(r_i\) 。

考虑一个矩形 \(M_{i,j}\) 表示 \(i\) 可以出发到 \(j\) 的时刻数。

断开：

如果在 \([l,r]\) 区间中，断了 \((x, x+1)\) 这条路，区间变为 \([l,x]\) 和 \([x+1,r]\)

那么在矩形中体现为：子矩形 \([(l,x+1),(x,r)]\) 全体减 \(q - 现在的时刻\)

连接：

如果在 \([l,x],[x+1,r]\) 区间中，连接了 \((x,x+1)\) 这条路，区间合并为 \([l,r]\)

那么在矩形中体现为：子矩形 \([(l,x+1),(x,r)]\) 全体加 \(q - 现在的时刻\)

这里的全体加/减本质为差分思想，连接/断开可以用 \(set\) 维护。

对于查询，本质上就是求前缀矩形 \([(1, 1), (a,b)]\) 的和。

需要注意的是，如果当前 \(a\) 和 \(b\) 连通，则需要给计算的答案减去 \(q - 现在的时刻\)。

树套树即可，我用的是树状数组套动态开点线段树。

当然也可以离线跑 \(CDQ\) ，空间会省一点。

时间复杂度：\(O(nlog^2n)\)