C基础 寻找随机函数的G点

引言

　　随机函数算法应该是计算机史上最重要的十大算法之一吧. 而C中使用的随机函数

#include <stdlib.h>

_Check_return_ _ACRTIMP int __cdecl rand(void);

本文主要围绕rand 函数找到G点. 就是伪随机函数的周期值.

关于rand 源码, 可以从Linux底层源码 glibc中找.  看了一下大约4个文件. 算法比较复杂. 感觉很稳定.

这里不探讨随机算法的实现. 只为了找到 随机函数周期.

前言

　　现在window上测试. 测试代码 main.c

#include <stdio.h>
#include <stdlib.h>

#define _INT_R        (128)
#define _INT_FZ        (10000000)

// 得到rand() 返回值, 并写入到文件中
int getrand(long long *pcut) {
    static int _cut = ;
    long long t = *pcut + ;

    int r = rand();

    // 每次到万再提醒一下
    if(t % _INT_FZ == )
        fprintf(stdout, "%d 个数据跑完了[%d, %lld]\n", _INT_FZ, _cut, t);

    if(t < ) { // 数据超标了
        ++_cut;
        fprintf(stderr, "Now %d T > %lld\n", _cut, t - );
        *pcut = ; // 重新开始一轮
    }

    *pcut = t;
    return r;
}

/*
 * 验证 rand 函数的周期
 */
int main(int argc, char* argv[]) {
    int rbase[_INT_R];
    int i = -, r;
    long long cut = ;

    // 先产生随机函数
    while(++i < _INT_R)
        rbase[i] = getrand(&cut);

    // 这里开始随机了
    for(;;) {
        r = getrand(&cut);
        if (r != rbase[])
            continue;

        for(i=; i<_INT_R; ++i) {
            r = getrand(&cut);
            if(r != rbase[i])
                break;
        }

        // 找见了数据
        if(i == _INT_R) {
            printf("Now T = %lld\n", cut);
            break;
        }
    }

    system("pause");
    return ;
}

主要思路是 _INT_R 128个数重叠那我们就认为. 已经找到这个周期了.

测试结果截图是

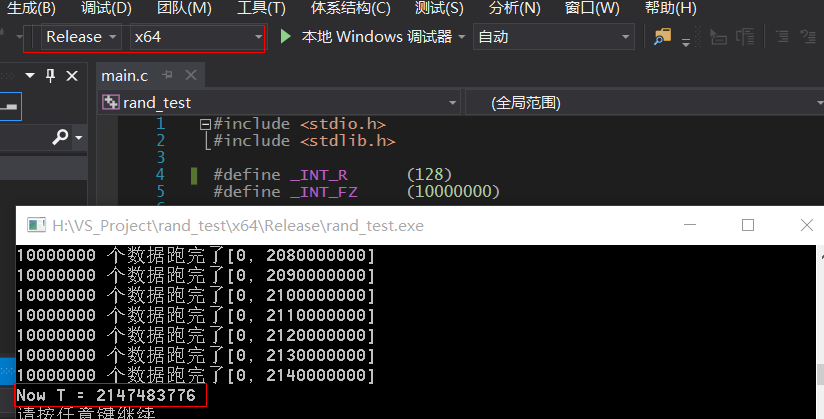
主要采用 Release  X64 编译. 为了检验上面结果是可以接受的, 将 _INT_R 改成1024 重新编译一次.

运行结果如下:

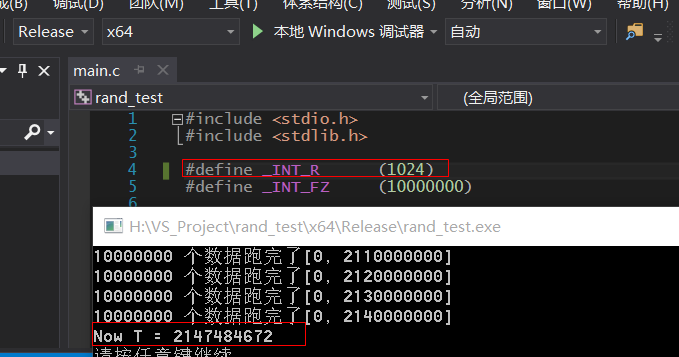
综合上面我们找见了 window 上 rand 函数的 G点 是

2147483776 - 128 =  214748248

2147484672 - 1024 = 2147483648

因而得到 window 上 VS2015 编译器的 rand G点 是 2147483648.

G点在游戏中用的很多. 例如抽奖, 掉装备, 暴击等等.

正文

1. 在linux 上试试水

　　在linux上试试 测试代码基本一样 rand2.c 如下

#include <stdio.h>
#include <stdlib.h>

#define _INT_R        (1024)
#define _INT_FZ        (100000000)

// 得到rand() 返回值, 并写入到文件中
int getrand(long long *pcut) {
    static int _cut = ;
    long long t = *pcut + ;

    int r = rand();

    // 每次到万再提醒一下
    if(t % _INT_FZ == )
        fprintf(stdout, "%d个数据又跑完了[%d, %lld]\n", _INT_FZ, _cut, t);

    if(t < ) { // 数据超标了
        ++_cut;
        fprintf(stderr, "Now %d T > %lld\n", _cut, t - );
        *pcut = ; // 重新开始一轮
    }

    *pcut = t;
    return r;
}

/*
 * 验证 rand 函数的周期
 */
int main(int argc, char* argv[]) {
    int rbase[_INT_R];
    int i = -, r;
    long long cut = ;

    // 先产生随机函数
    while(++i < _INT_R)
        rbase[i] = getrand(&cut);

    // 这里开始随机了
    for(;;) {
        r = getrand(&cut);
        if (r != rbase[])
            continue;

        for(i=; i<_INT_R; ++i) {
            r = getrand(&cut);
            if(r != rbase[i])
                break;
        }

        // 找见了数据
        if(i == _INT_R) {
            printf("Now T = %lld\n", cut);
            break;
        }
    }

    return ;
}

编译命令

gcc - -o randc2.out rand2.c

最后运行结果, 等了 好久还是没出来.

Linux 上的rand 函数写的很有水准, 分布的很随机. 总而言之这个随机值比较大. 但一定存在的.

有兴趣的可以按照上面思路优化跑一跑. 这边Ubuntu 是虚拟机跑的慢.

2. 继续扩展, 减小rand 返回 MAX值 试试水

　　修改上面 getrand  函数

// _INT_RMAX 表示随机数范围 [0, 100)
#define _INT_RMAX    (100)
#define _INT_R        (1024)
#define _INT_FZ        (10000000)

// 得到rand() 返回值, 并写入到文件中
int getrand(long long *pcut) {
    static int _cut = ;
    long long t = *pcut + ;

    int r = rand() % _INT_RMAX;

    // 每次到万再提醒一下
    if (t % _INT_FZ == )
        fprintf(stdout, "%d 个数据跑完了[%d, %lld]\n", _INT_FZ, _cut, t);

    if (t < ) { // 数据超标了
        ++_cut;
        fprintf(stderr, "Now %d T > %lld\n", _cut, t - );
        *pcut = ; // 重新开始一轮
    }

    *pcut = t;
    return r;
}

添加 了 取余看是否, 影响G点 测试结果

　　

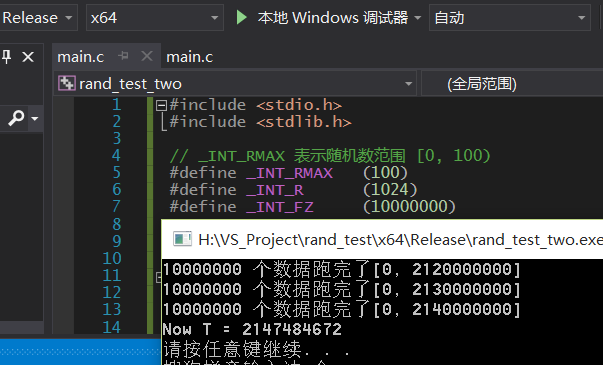
发现G点没有变化.

可以有推论: rand() 周期不随着 二次 mod取余而改变.

因而可以放心 mod使用 伪随机函数. G点还是那么大.

3. 最后, 赠送一个常用的 [min, max] 之间的随机函数

/*
 * 返回 [min, max] 区间的随机函数
 * min    : 起始位置
 * max    : 结束位置
 *        : 返回[min, max]区间之内的位置
 */
extern int random(int min, int max);

/*
 * 返回 [min, max] 区间的随机函数
 * min    : 起始位置
 * max    : 结束位置
 *        : 返回[min, max]区间之内的位置
 */
int
random(int min, int max) {
    assert(min < max);
    // 正常情况
    return rand() % (max - min + ) + min;
}

测试demo 代码 结构如下

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <assert.h>

/*
 * 返回 [min, max] 区间的随机函数
 * min    : 起始位置
 * max    : 结束位置
 *        : 返回[min, max]区间之内的位置
 */
extern int random(int min, int max);

/*
 * C 基础, 使用随机函数
 */
int main(int argc, char* argv[]) {

    int min = -, max = ;
    int i = ;

    // 开始统一 初始化种子
    srand((unsigned)time(NULL));

    while(i < ) {
        printf("%3d ", random(min, max));
        if (++i %  == )
            putchar('\n');
    }

    system("pause");
    return ;
}

/*
 * 返回 [min, max] 区间的随机函数
 * min    : 起始位置
 * max    : 结束位置
 *        : 返回[min, max]区间之内的位置
 */
int
random(int min, int max) {
    assert(min < max);
    // 正常情况
    return rand() % (max - min + ) + min;
}

测试结果是

基本比较稳定. 一切都在预料之中.

总结 本文 得出两个 推论

　　a. rand()伪随机函数, 存在G点. 并且可以找到

　　b. G点 不随着 二次 mod 取余改变.

后记

　　错误是难免的, 预祝明天愉快~~