HDU5742 It's All In The Mind 数学思维题

Problem Description

Professor Zhang has a number sequence a1,a2,...,an. However, the sequence is not complete and some elements are missing. Fortunately, Professor Zhang remembers some properties of the sequence:

1. For every i∈{1,2,...,n}, 0≤ai≤100.
2. The sequence is non-increasing, i.e. a1≥a2≥...≥an.
3. The sum of all elements in the sequence is not zero.

Professor Zhang wants to know the maximum value of a1+a2∑ni=1ai among all the possible sequences.

 

Input

There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:

The first contains two integers n and m (2≤n≤100,0≤m≤n) -- the length of the sequence and the number of known elements.

In the next m lines, each contains two integers xi and yi (1≤xi≤n,0≤yi≤100,xi<xi+1,yi≥yi+1), indicating that axi=yi.

 

Output

For each test case, output the answer as an irreducible fraction "p/q", where p, q are integers, q>0.

 

Sample

Sample Input

Sample Output
/
/

题意：

　　有一个数字序列，给出数字序列的性质是：

　　1.每个数最大为100，最小为0

　　2.序列非递增

　　3.序列总和不为0

　　求出这个数列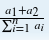的最大值

　　样例：第一行是T，表示T组测试样例，第二行是n，m。表示序列的长度和已知数的个数。下m行为xy，表示a_xi=yi

　　　　　　第一组 长度为2，已知0个。则最大值为（100+100）/（100+100）或者（1+1）/（1+1）最大值为1。

　　　　　　第二组长度为3，已知1个。已知的这一个为a₃=1 。则最大值为（100+100）/（100+100+1）

思路：

　　想求（a1+a2)/(a1+a2+...+an) 的最大值，只要让分母尽可能大，分子尽可能小即可。

　　有两种情况，第一种为已知a1，a2。让不知道的数取最小值（不是0，因为要保证序列非递增）。

　　第二种情况，不知道a1或者a2。让a1和a2取最大值（也要注意序列非递增）。

　　最后用GCD求出a1+a2与序列和的最大公因数，然后取分数。

代码：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
int gcd(int a,int b)//求最大公约数
{
    if(b==)
        return a;
    return gcd(b,a%b);
}
int main()
{
    int a[],t,m,n;
    scanf("%d",&t);
    while(t--)
    {
        int i,j,x,y,sum1=,sum2=,ans=;
        int w=;
        scanf("%d%d",&n,&m);
        for(i=; i<=n; i++)
            a[i]=-;//初始化数组为-1，因为数组从0-100，所以可以用-1来表示
        for(i=; i<=m; i++)
        {
            scanf("%d%d",&x,&y);
            a[x]=y;//将已知条件赋值
        }
        for(i=n; i>=; i--)//从3-n尽量取最小
        {
            if(a[i]==-)//如果后面没有值，说明没有非递增限制，直接赋值为w，w初始为0
                a[i]=w;
            else//如果已经有值，则值前面的赋值为这个值。
            {
                w=a[i];
            }
        }
        if(a[]==-)/*如果a[1]没有值，则赋值为100（最大）*/
            a[]=;
        if(a[]==-)/*如果a[2]没有值，则与a[1]相同*/
            a[]=a[];
        for(i=; i<=n; i++)
            sum1+=a[i];
        sum2=a[]+a[];
        ans=gcd(sum2,sum1);
        printf("%d/%d\n",(sum2/ans),(sum1/ans));
    }
}