【15】【有点特殊的dp】 剪绳子

题目

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m] 。请问 k[0]k[1]...*k[m] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/jian-sheng-zi-lcof

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

我一开始以为是普通dp

忽略了一个要点，那就是，这类题的dp[i-j]有两种状态，可拆分和不再拆分

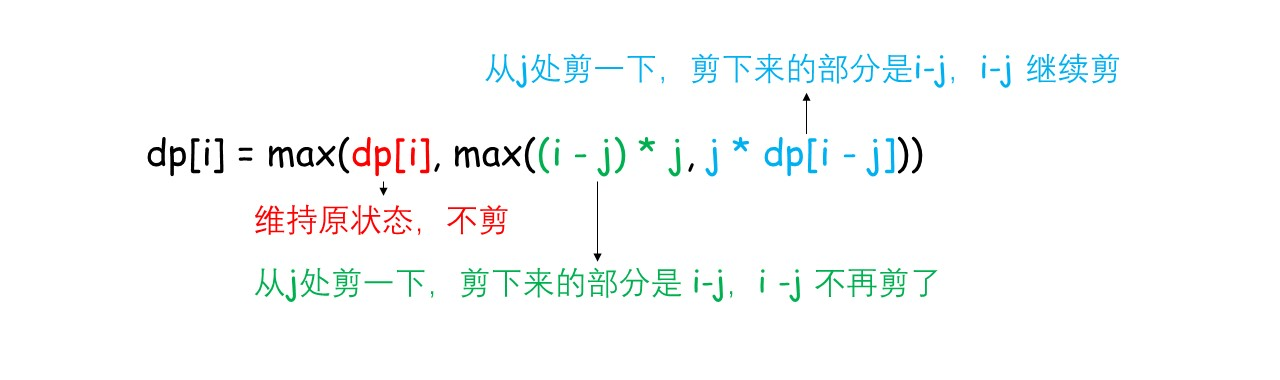
收获

特殊DP，这种去区间题记得在dp方程内再设一个max()

代码

class Solution {

    //dp[n]:长度为n的绳子的最大乘积
    //dp[1]=1.dp[2]=1

    public int[] dp;
    public int cuttingRope(int n) {
        dp=new int[n+1];
        dp[1] =1;dp[2]=1;
        for(int i= 2;i<n+1;i++){
            for(int j=1;j<i+1&&(i-j)>0;j++){
                    dp[i] =Math.max(dp[i],Math.max((i-j)*j,j*dp[i-j]));
            }
        }
        return dp[n];
    }
}