Luogu P2458 [SDOI2006]保安站岗(树形dp)

P2458 [SDOI2006]保安站岗

题意

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

第\(1\)行\(n\)，表示树中结点的数目。

第\(2\)行至第\(n+1\)行，每行描述每个通道端点的信息，依次为：该结点标号\(i(0<i\leq n)\)，在该结点安置保安所需的经费\(k(k\leq 10000)\)，该边的儿子数\(m\)，接下来\(m\)个数，分别是这个节点的\(m\)个儿子的标号\(r_1,r_2,\dots ,r_m\)。

对于一个\(n(0<n\leq 1500)\)个结点的树，结点标号在\(1\)到\(n\)之间，且标号不重复。

输出格式：

最少的经费。

如右图的输入数据示例

输出数据示例：

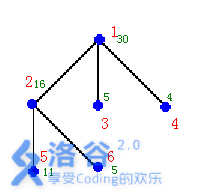
输入输出样例

输入样例#1：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例#1：

25

说明

样例说明：在结点\(2,3,4\)安置\(3\)个保安能看守所有的\(6\)个结点，需要的经费最小：\(25\)

思路

开始复健树形\(dp\)。

对于每一个结点，可能有三种保护状态：被儿子保护，被自己保护，被父亲保护。所以我们可以这样设计状态：\(f[i][0/1/2]\)表示结点\(i\)的三种状态下的子树最小经费要求。在下面的代码中，\(0\)表示被父亲保护，\(1\)表示被儿子保护，\(2\)表示被自己保护。转移方程也很简单了。

void dfs(int now)
{
    dp[now][0]=0,dp[now][1]=0x3f3f3f3f,dp[now][2]=val[now];//初始值
    for(int i=top[now];i;i=nex[i])
    {
        dfs(to[i]);
        dp[now][0]+=min(dp[to[i]][1],dp[to[i]][2]);//儿子不可能被自己保护
        dp[now][2]+=min(dp[to[i]][0],min(dp[to[i]][1],dp[to[i]][2]));//儿子的保护状态可以随意选择。
    }
    for(int i=top[now];i;i=nex[i]) dp[now][1]=min(dp[now][1],dp[now][0]-min(dp[to[i]][1],dp[to[i]][2])+dp[to[i]][2]);//相当于直接记录最大花费的儿子
}

AC代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1505;
int n,val[MAXN],dp[MAXN][3];
int cnt,top[MAXN],to[MAXN],nex[MAXN];
bool vis[MAXN];
int read()
{
    int re=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void dfs(int now)
{
    dp[now][0]=0,dp[now][1]=0x3f3f3f3f,dp[now][2]=val[now];
    for(int i=top[now];i;i=nex[i])
    {
        dfs(to[i]);
        dp[now][0]+=min(dp[to[i]][1],dp[to[i]][2]);
        dp[now][2]+=min(dp[to[i]][0],min(dp[to[i]][1],dp[to[i]][2]));
    }
    for(int i=top[now];i;i=nex[i]) dp[now][1]=min(dp[now][1],dp[now][0]-min(dp[to[i]][1],dp[to[i]][2])+dp[to[i]][2]);
}
int main()
{
    n=read();
    for(int i=0;i<n;i++)
    {
        int x=read();val[x]=read();int j=read();
        while(j--)
        {
            int y=read();vis[y]=true;
            to[++cnt]=y,nex[cnt]=top[x],top[x]=cnt;
        }
    }
    for(int i=1;i<=n;i++)
        if(!vis[i])
        {
            dfs(i);
            printf("%d",min(dp[i][1],dp[i][2]));
            return 0;
        }
}