有向图的拓扑排序算法JAVA实现

一，问题描述

给定一个有向图G=（V,E），将之进行拓扑排序，如果图有环，则提示异常。

要想实现图的算法，如拓扑排序、最短路径……并运行看输出结果，首先就得构造一个图。由于构造图的方式有很多种，这里假设图的数据存储在一个文件中，

每一行包含如下的信息：
LinkID,SourceID,DestinationID,Cost
其中，LinkID为该有向边的索引，SourceID为该有向边的起始顶点的索引，DestinationID为该有向边的终止顶点的索引，Cost为该有向边的权重。

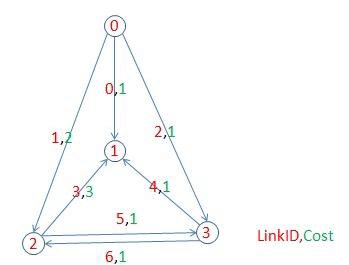
0,0,1,1
1,0,2,2
2,0,3,1
3,2,1,3
4,3,1,1
5,2,3,1
6,3,2,1

(以上示例引用自网上，该图仅用来表示存储图信息的文件内容的格式，对拓扑排序而言，上图显然存在环)

对于以下的拓扑排序程序，只用到了SourceID，和DestionatinID这两个字段。拓扑序列以顶点的索引表示。后续会实现无向图的最短路径算法，就会用到Cost这个字段啦！！！

二，算法实现思路

拓扑排序，其实就是寻找一个入度为0的顶点，该顶点是拓扑排序中的第一个顶点序列，将之标记删除，然后将与该顶点相邻接的顶点的入度减1，再继续寻找入度为0的顶点，直至所有的顶点都已经标记删除或者图中有环。

从上可以看出，关键是寻找入度为0的顶点。

一种方式是遍历整个图中的顶点，找出入度为0的顶点，然后标记删除该顶点，更新相关顶点的入度，由于图中有V个顶点，每次找出入度为0的顶点后会更新相关顶点的入度，因此下一次又要重新扫描图中所有的顶点。故时间复杂度为O(V^2)

由于删除入度为0的顶点时，只会更新与它邻接的顶点的入度，即只会影响与之邻接的顶点。但是上面的方式却遍历了图中所有的顶点的入度。

改进的另一种方式是：先将入度为0的顶点放在栈或者队列中。当队列不空时，删除一个顶点v，然后更新与顶点v邻接的顶点的入度。只要有一个顶点的入度降为0，则将之入队列。此时，拓扑排序就是顶点出队的顺序。该算法的时间复杂度为O（V+E）

三，拓扑排序方法的实现

该算法借助队列来实现时，感觉与 二叉树的 层序遍历算法很相似啊。说明这里面有广度优先的思想。

第一步：遍历图中所有的顶点，将入度为0的顶点 入队列。

第二步：从队列中出一个顶点，打印顶点，更新该顶点的邻接点的入度(减1)，如果邻接点的入度减1之后变成了0，则将该邻接点入队列。

第三步：一直执行上面 第二步，直到队列为空。

     public void topoSort() throws Exception{
         int count = 0;//判断是否所有的顶点都出队了,若有顶点未入队(组成环的顶点)，则这些顶点肯定不会出队
 
         Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
         //扫描所有的顶点,将入度为0的顶点入队列
         Collection<Vertex> vertexs = directedGraph.values();
         for (Vertex vertex : vertexs)
             if(vertex.inDegree == 0)
                 queue.offer(vertex);
         //度为0的顶点出队列并且更新它的邻接点的入度
         while(!queue.isEmpty()){
             Vertex v = queue.poll();
             System.out.print(v.vertexLabel + " ");//输出拓扑排序的顺序
             count++;
             for (Edge e : v.adjEdges)
                 if(--e.endVertex.inDegree == 0)
                     queue.offer(e.endVertex);
         }
         if(count != directedGraph.size())
             throw new Exception("Graph has circle");
     }

第7行for循环：先将图中所有入度为0的顶点入队列。

第11行while循环：将入度为0的顶点出队列，并更新与之邻接的顶点的入度，若邻接顶点的入度降为0，则入队列（第16行if语句）。

第19行if语句判断图中是否有环。因为，只有在每个顶点出队时，count++。对于组成环的顶点，是不可能入队列的，因为组成环的顶点的入度不可能为0（第16行if语句不会成立）.

因此，如果有环，count的值 一定小于图中顶点的个数。

四，完整代码实现

DirectedGraph.java中定义了图 数据结构，（图的实现可参考：数据结构--图 的JAVA实现(上)）。并根据FileUtil.java中得到的字符串构造图。

构造 图之后，topoSort方法实现了拓扑排序。

 import java.util.Collection;
 import java.util.LinkedHashMap;
 import java.util.LinkedList;
 import java.util.List;
 import java.util.Map;
 import java.util.Queue;
 
 /*
  * 用来实现拓扑排序的有向无环图
  */
 public class DirectedGraph {
 
     private class Vertex{
         private String vertexLabel;// 顶点标识
         private List<Edge> adjEdges;
         private int inDegree;// 该顶点的入度
 
         public Vertex(String verTtexLabel) {
             this.vertexLabel = verTtexLabel;
             inDegree = 0;
             adjEdges = new LinkedList<Edge>();
         }
     }
 
     private class Edge {
         private Vertex endVertex;
 
         // private double weight;
         public Edge(Vertex endVertex) {
             this.endVertex = endVertex;
         }
     }
 
     private Map<String, Vertex> directedGraph;
 
     public DirectedGraph(String graphContent) {
         directedGraph = new LinkedHashMap<String, DirectedGraph.Vertex>();
         buildGraph(graphContent);
     }
 
     private void buildGraph(String graphContent) {
         String[] lines = graphContent.split("\n");
         Vertex startNode, endNode;
         String startNodeLabel, endNodeLabel;
         Edge e;
         for (int i = 0; i < lines.length; i++) {
             String[] nodesInfo = lines[i].split(",");
             startNodeLabel = nodesInfo[1];
             endNodeLabel = nodesInfo[2];
             startNode = directedGraph.get(startNodeLabel);
             if(startNode == null){
                 startNode = new Vertex(startNodeLabel);
                 directedGraph.put(startNodeLabel, startNode);
             }
             endNode = directedGraph.get(endNodeLabel);
             if(endNode == null){
                 endNode = new Vertex(endNodeLabel);
                 directedGraph.put(endNodeLabel, endNode);
             }
 
             e = new Edge(endNode);//每读入一行代表一条边
             startNode.adjEdges.add(e);//每读入一行数据,起始顶点添加一条边
             endNode.inDegree++;//每读入一行数据,终止顶点入度加1
         }
     }
 
     public void topoSort() throws Exception{
         int count = 0;
 
         Queue<Vertex> queue = new LinkedList<>();// 拓扑排序中用到的栈,也可用队列.
         //扫描所有的顶点,将入度为0的顶点入队列
         Collection<Vertex> vertexs = directedGraph.values();
         for (Vertex vertex : vertexs)
             if(vertex.inDegree == 0)
                 queue.offer(vertex);
 
         while(!queue.isEmpty()){
             Vertex v = queue.poll();
             System.out.print(v.vertexLabel + " ");
             count++;
             for (Edge e : v.adjEdges)
                 if(--e.endVertex.inDegree == 0)
                     queue.offer(e.endVertex);
         }
         if(count != directedGraph.size())
             throw new Exception("Graph has circle");
     }
 }

FileUtil.java负责从文件中读取图的信息。将文件内容转换成 第一点 中描述的字符串格式。--该类来源于网络

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.Closeable;
import java.io.File;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
 
public final class FileUtil
{
    /**
     * 读取文件并按行输出
     * @param filePath
     * @param spec 允许解析的最大行数， spec==null时，解析所有行
     * @return
     * @author
     * @since 2016-3-1
     */
    public static String read(final String filePath, final Integer spec)
    {
        File file = new File(filePath);
        // 当文件不存在或者不可读时
        if ((!isFileExists(file)) || (!file.canRead()))
        {
            System.out.println("file [" + filePath + "] is not exist or cannot read!!!");
            return null;
        }
 
        BufferedReader br = null;
        FileReader fb = null;
        StringBuffer sb = new StringBuffer();
        try
        {
            fb = new FileReader(file);
            br = new BufferedReader(fb);
 
            String str = null;
            int index = 0;
            while (((spec == null) || index++ < spec) && (str = br.readLine()) != null)
            {
                sb.append(str + "\n");
//                System.out.println(str);
 
            }
        }
        catch (IOException e)
        {
            e.printStackTrace();
        }
        finally
        {
            closeQuietly(br);
            closeQuietly(fb);
        }
 
        return sb.toString();
    }
    /**
     * 写文件
     * @param filePath 输出文件路径
     * @param content 要写入的内容
     * @param append 是否追加
     * @return
     * @author s00274007
     * @since 2016-3-1
     */
    public static int write(final String filePath, final String content, final boolean append)
    {
        File file = new File(filePath);
        if (content == null)
        {
            System.out.println("file [" + filePath + "] invalid!!!");
            return 0;
        }
 
        // 当文件存在但不可写时
        if (isFileExists(file) && (!file.canRead()))
        {
            return 0;
        }
 
        FileWriter fw = null;
        BufferedWriter bw = null;
        try
        {
            if (!isFileExists(file))
            {
                file.createNewFile();
            }
 
            fw = new FileWriter(file, append);
            bw = new BufferedWriter(fw);
 
            bw.write(content);
        }
        catch (IOException e)
        {
            e.printStackTrace();
            return 0;
        }
        finally
        {
            closeQuietly(bw);
            closeQuietly(fw);
        }
 
        return 1;
    }
 
    private static void closeQuietly(Closeable closeable)
    {
        try
        {
            if (closeable != null)
            {
                closeable.close();
            }
        }
        catch (IOException e)
        {
        }
    }
 
    private static boolean isFileExists(final File file)
    {
        if (file.exists() && file.isFile())
        {
            return true;
        }
 
        return false;
    }
}

测试类：TestTopoSort.java

 public class TestTopoSort {
     public static void main(String[] args) {
         String graphFilePath;
         if(args.length == 0)
             graphFilePath = "F:\\xxx";
         else
             graphFilePath = args[0];
 
         String graphContent = FileUtil.read(graphFilePath, null);//从文件中读取图的数据
         DirectedGraph directedGraph = new DirectedGraph(graphContent);
         try{
             directedGraph.topoSort();
         }catch(Exception e){
             System.out.println("graph has circle");
             e.printStackTrace();
         }
     }
 }