OpenGL列主元矩阵和列主序存储

OpenGL矩阵要考虑两个点，一个是向量如何排布，一个是矩阵如何存储和恢复。

1.排布

排布决定了运算的顺序。OpenGL使用的是列主元，它的意思就是一个4X4的矩阵是由4个列向量构成（这里的v1,v2,v3的x,y,z分量构成的向量其实分别对应新坐标系下的三个轴，v4的x,y,z分量对应平移量）：

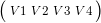
对一个列向量进行变换即：

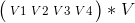
举个例子，比如做平移：

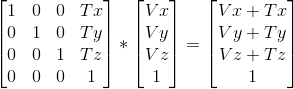
2.存储和恢复

矩阵一般都存储在连续内存中，最初如何存放决定了之后在GLSL中如何恢复。

可以这样存储（行主序）--记为Mat1

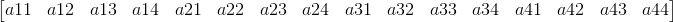
也可以这样存储（列主序）--记为Mat2

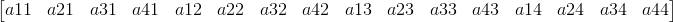
数据传入着色器是这样排布的

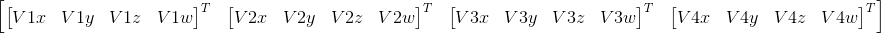
就是传进显存的连续数据直接分成4个列向量，也就是

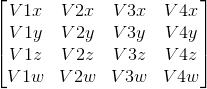
所以

Mat1在GLSL中的样子就是

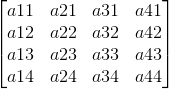
和原来的矩阵比起来，它发生了转置，所以如果glUniformMatrix4fv()中transpose参数设置为GL_TRUE，则会做一次转置，恢复成

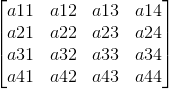
而Mat2不需要设置transpose为GL_TRUE。你可以认为它在存储的时候已经做了转置。

根本原因是内存是行主序的，而GLSL是列主序的，所以有一个转置的过程。（HLSL是行主序的，与内存排布一致，所以不需要考虑这个问题。）