java基础---数组的查找算法(2)
一、查找的基本概念
查找分为有序查找和无序查找,这里均以数组为对象,有序查找指的是数组元素有序排列,无序查找指的是数组元素有序或无序排列
- 平均查找长度(Average Search Length,ASL):和指定查找元素key进行比较的表中数据的个数的期望值
对于含有n个数据元素的查找表,查找成功的平均查找长度为:
ASL = Pi*Ci的和。Pi:查找表中第i个数据元素的概率。
Ci:找到第i个数据元素时已经比较过的次数。
- 查找分类:线性查找(顺序查找)、二分查找(折半查找)、插值查找、斐波那契查找、分块查找、哈希查找、二叉树查找
- 查找性能从慢到快:
- 顺序查找,时间复杂度O(N)
分块查找,时间复杂度O(logN+N/m);
二分查找,时间复杂度O(logN)
Fibonacci查找,时间复杂度O(logN)
插值查找,时间复杂度O(log(logN))
哈希查找,时间复杂度O(1)
二、 线性查找
顺序查找适合于存储结构为顺序存储或链接存储的线性表,即查找对象存储空间连续
时间复杂度为O(n)
查找成功时的平均查找长度为:(假设每个数据元素的概率相等)
ASL =(1+2+3+…+n)/n = (n+1)/2 ;当查找不成功时,需要n+1次比较,时间复杂度为O(n);
package Search; import java.util.ArrayList;
import java.util.List; public class LinearSearch { public static void main(String[] args) {
int[] arr={1,9,19,0,-2,9,43};
System.out.println(firstlinearSearch(arr,-2));
System.out.println(lastlinearSearch(arr,-1));
System.out.println(repeatlinearSearch(arr,9));
}
//返回顺序查找第一次找到的下标位置
private static int firstlinearSearch(int[] arr, int key) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == key) {
return i;
}
}
return -1;}
//返回顺序查找最后一次找到的下标位置
private static int lastlinearSearch(int[] arr, int key) {
int index=-1;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == key) {
index=i;
}
}
return index;
}
//返回所有重复的元素下标
private static List<Integer> repeatlinearSearch(int[] arr, int key) {
List<Integer> list= new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if (arr[i] == key) {
list.add(i);
}
}
return list;
}
}
三、 二分查找
折半查找,属于有序查找算法。这里的有序是指查找的数组元素是有序排列的
用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,
递归思想
递归条件:查找值>中间值, 向右递归;查找值<中间值, 向左递归
终止条件:查找值=中间值, 返回中间值坐标; 查找区间溢出(left>right), 返回-1;
- 如果有溢出,说明left+right>Integer.MAX_VALUE
对待有重复元素的数组:当 查找值=中间值, 在中间值坐标向左向右遍历(temp>left && arr[temp]==arr[mid];temp<right&&arr[temp]=arr[mid]),直到找到与中间值不相等的元素,顺序添加到表中
- 非递归思想,直接用循环while(left<right)
- 查找值>中间值, left=mid; 查找值<中间值, right=mid;
- 终止条件:查找值=中间值, 返回中间值坐标; 查找区间溢出(left>right), 返回-1;
最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n);
折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。
但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用
package Search;
import java.util.ArrayList;
import java.util.List;
public class BinarySearch {
public static void main(String[] args) {
int[] arr={1,2,3,4,5,6,7,8,8,8,10,23,45,67,89,100,101};
System.out.println(binarysearch(arr,0,arr.length-1,8));
System.out.println(repeatbinarysearch(arr,0,arr.length-1,8));
System.out.println(bobinarysearch(arr,0,arr.length-1,8));
} //返回所有与查找元素相同的所有元素下标
private static List<Integer> repeatbinarysearch(int[] arr, int left, int right, int key) {
if (left>right) return new ArrayList<>();
List<Integer> list= new ArrayList<>();
int mid=(left+right)/2;
if (arr[mid]<key){
return repeatbinarysearch(arr,mid+1,right,key);
}else if (key<arr[mid]){
return repeatbinarysearch(arr,left,mid-1,key);
}else {
int temp=mid-1;
while (true) {
if (temp < left || arr[temp] != arr[mid]) {
break;
}
else temp--;
}
for (int i= temp+1;i<mid;i++){
list.add(i);
}
temp=mid;
while (true) {
if (temp >right || arr[temp] != arr[mid]) {
break;
}
else {list.add(temp);
temp++;}
}
return list;
}
} //不一定返回的是顺序第一次找到的下标
private static int binarysearch(int[] arr, int left, int right, int key) {
if (left>right) return -1;
int mid= (left+right)/2;
if (arr[mid]<key){
return binarysearch(arr,mid+1,right,key);
}else if (key < arr[mid]){
return binarysearch(arr,left,mid-1,key);
}else return mid;
}
//非递归
private static int bobinarysearch(int[] arr, int left, int right, int key) {
if (arr==null||arr.length==0) return -1;
if (left>right) return -1;
int mid;
while (left<right){
mid=left+(right-left)/2;
if (arr[mid]==key)return mid;
else if(arr[mid]<key) left=mid+1;
else right=mid-1;
}
return -1;
}
}
四、 插值查找
基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率,属于有序查找
查找成功或者失败的时间复杂度均为O(log2(log2n))
对于表长较大,而关键字分布又比较均匀的查找表来说,插值查找算法的平均性能比折半查找要好的多。
反之,数组中如果分布非常不均匀,那么插值查找未必是很合适的选择。
与二分查找唯一的不同点是中值的选择利用了自适应算法 mid=left+(right-left) *(key-arr[left])/(arr[right]-arr[left])
package Search; import java.util.ArrayList;
import java.util.List; public class InsertValueSearch {
public static void main(String[] args) {
int[] arr=new int[100];
for (int i=0;i<arr.length;i++){
arr[i]=i+1;
}
arr[8]=8;
System.out.println(insertsearch(arr,0,arr.length-1,8));
System.out.println(repeatinsertsearch(arr,0,arr.length-1,8)); } private static List<Integer> repeatinsertsearch(int[] arr, int left, int right, int key) {
if (left > right) return new ArrayList<>();
List<Integer> list = new ArrayList<>();
//唯一的不同点是中值的选择利用了自适应算法
//low + (high-low) * (value-a[low]) / (a[high]-a[low]);
int mid = left + (right - left) * (key - arr[left]) / (arr[right] - arr[left]);
if (arr[mid] < key) {
return repeatinsertsearch(arr, mid + 1, right, key);
} else if (key < arr[mid]) {
return repeatinsertsearch(arr, left, mid - 1, key);
} else {
int temp = mid - 1;
while (true) {
if (temp < left || arr[temp] != arr[mid]) {
break;
} else temp--;
}
for (int i = temp + 1; i < mid; i++) {
list.add(i);
}
temp = mid;
while (true) {
if (temp > right || arr[temp] != arr[mid]) {
break;
} else {
list.add(temp);
temp++;
}
}
return list;
}
}
private static int insertsearch(int[] arr, int left, int right, int key) {
if (left>right) return -1;
int mid=left+(right-left)*(key-arr[left])/(arr[right]-arr[left]) ;
if (arr[mid]<key){
return insertsearch(arr,mid+1,right,key);
}else if (key < arr[mid]){
return insertsearch(arr,left,mid-1,key);
}else return mid;
}
}
五、 斐波那契查找
黄金分割比例 :要求开始表中记录的个数为某个斐波那契数小1,n=F(k)-1;
最坏情况下,时间复杂度为O(log2n),且其期望复杂度也为O(log2n)。
生成的数组长度是f[k]-1而不是f[k]
f[k]-1=f[k-1]-1+f[k-2]-1+1,只要顺序表的长度为f[k]-1,就可以将其分为左右两端,左边端为f[k-1]-1,右边为f[k-2]-1,中间值mid= left+ f[k-1]-1
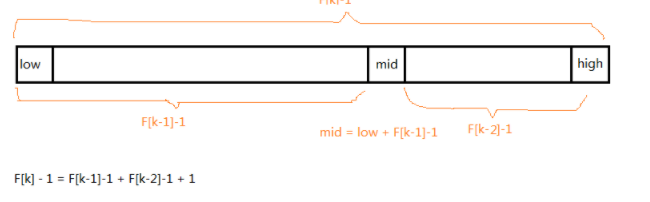
步骤:
生成一个斐波那次数组,这个数组的长度为f[k]-1
生成的数组很可能比要比较的数组元素大,因此要进行元素赋值和填充
package Search; import java.util.Arrays;
import java.util.List; public class FibonacciSearch {
public static void main(String[] args) {
int[] arr={1,2,3,4,5,6,7,8,8,8,10,23,45,67,89,100,101};
System.out.println(fibonacci(arr,100));
// System.out.println(repeatfibonacci(arr,8));
}
//构造斐波那次数组
private static int[] fib(int size) {
int[] f=new int[size];
f[0]=1;
f[1]=1;
for (int i=2;i<f.length;i++){
f[i]=f[i-1]+f[i-2];
}
return f;
}
private static int fibonacci(int[] arr, int key) {
int low = 0;
int high = arr.length-1;
int f[]= fib(arr.length);
//此时已经找到比high大的那个斐波那次点
int k=0;
while (high-low>f[k]-1) k++;
//复制一份arr,但长度可能有扩充
int[] temp = Arrays.copyOf(arr, f[k]);
//把扩充后的元素都赋值为当前数组的最大元素
for (int i=high;i<temp.length;i++) temp[i]=arr[high];
int mid=0;
while (low<=high){
mid= low + f[k-1]-1;
//此时f[k-1]指代的是左半部分
if (temp[mid]>key){
high=mid-1;
k--;
} //f[k-2]指代右半部分
else if (temp[mid] < key){
low=mid+1;
k-=2;
}
else return Math.min(mid, high);
}
return -1;
}
}
六、分块查找
分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。索引表就是帮助分块查找的一个分块依据,索引表是二分查找,而后进行顺序查找
分块查找只需要索引表有序,类似于哈希表,但又不如散列表好用。假设每个分块的长度为s,则分块查找的时间复杂度可以近似为:
,即
- 分块查找算法的查找算法并不复杂,复杂的时索引表的建立与维护,当元素加、减、修改时,如何保证各个分块之间依旧相对有序且各个分块的大小均匀,是分块查找算法最大的挑战
java基础---数组的查找算法(2)的更多相关文章
- java基础---数组的排序算法(3)
一.排序的基本概念 排序:将一个数据元素集合或序列重新排列成按一个数据元素某个数据项值有序的序列 稳定排序:排序前和排序后相同元素的位置关系与初始序列位置一致(针对重复元素来说,相对位置不变) 不稳定 ...
- java基础-数组的折半查找原理
java基础-数组的折半查找原理 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 如果让你写一个数组的查找功能,需求如下:在一个数组中,找一个元素,是否存在于数组中, 如果存在就返回 ...
- Java中常用的查找算法——顺序查找和二分查找
Java中常用的查找算法——顺序查找和二分查找 神话丿小王子的博客 一.顺序查找: a) 原理:顺序查找就是按顺序从头到尾依次往下查找,找到数据,则提前结束查找,找不到便一直查找下去,直到数据最后一位 ...
- Java学习之二分查找算法
好久没写算法了.只记得递归方法..结果测试下爆栈了. 思路就是取范围的中间点,判断是不是要找的值,是就输出,不是就与范围的两个临界值比较大小,不断更新临界值直到找到为止,给定的集合一定是有序的. 自己 ...
- Java基础——数组应用之StringBuilder类和StringBuffer类
接上文:Java基础——数组应用之字符串String类 一.StringBuffer类 StringBuffer类和String一样,也用来代表字符串,只是由于StringBuffer的内部实现方式和 ...
- Java基础-数组常见排序方式
Java基础-数组常见排序方式 作者:尹正杰 版权声明:原创作品,谢绝转载!否则将追究法律责任. 数据的排序一般都是生序排序,即元素从小到大排列.常见的有两种排序方式:选择排序和冒泡排序.选择排序的特 ...
- 《Java基础——数组的定义与使用》
Java基础--数组的定义与使用 一. 一维数组: 格式一: 数组类型 数组变量[]=new 数据类型[长度]; //需要后续赋值,且后续赋值时只能为单个元素赋值. 或 数组类型 数组变量 ...
- Java实现的二分查找算法
二分查找又称折半查找,它是一种效率较高的查找方法. 折半查找的算法思想是将数列按有序化(递增或递减)排列,查找过程中采用跳跃式方式查找,即先以有序数列的中点位置为比较对象,如果要找的元素值小 于该中点 ...
- Java基础(50):二分法查找的非递归实现和递归实现(完整代码可运行,参考VisualGO理解更佳)
一.概念 二分查找算法也称折半查找,是一种在有序数组中查找某一特定元素的搜索算法. 二.算法思想 搜素过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束:如果某一特定元素大于或者 ...
随机推荐
- 26.Qt Quick QML-RotationAnimation、PathAnimation、SmoothedAnimation、Behavior、PauseAnimation、SequentialAnimation和ParallelAnimation
1.RotationAnimationRotationAnimation也是继承于PropertyAnimation组件,但是它有点特殊,它只需要指定taget目标对象,并且不需要指定property ...
- Locust入门
Locust入门 Locust是一款Python技术栈的开源的性能测试工具.Locust直译为蝗虫,寓意着它能产生蝗虫般成千上万的并发用户: Locust并不小众,从它Github的Star数量就 ...
- GO学习-(35) Go实现日志收集系统4
Go实现日志收集系统4 到这一步,我的收集系统就已经完成很大一部分工作,我们重新看一下我们之前画的图: 我们已经完成前面的部分,剩下是要完成后半部分,将kafka中的数据扔到ElasticSear ...
- GO学习-(29) Go语言操作etcd
Go语言操作etcd etcd是近几年比较火热的一个开源的.分布式的键值对数据存储系统,提供共享配置.服务的注册和发现,本文主要介绍etcd的安装和使用. etcd etcd介绍 etcd是使用Go语 ...
- 为什么edge AI是一个无需大脑的人
为什么edge AI是一个无需大脑的人 Why edge AI is a no-brainer 德勤预计,到2020年,将售出超过7.5亿个edge AI芯片,即在设备上而不是在远程数据中心执行或加速 ...
- Java 并发基础知识
一.什么是线程和进程? 进程: 是程序的一次执行过程,是系统运行程序的基本单元(就比如打开某个应用,就是开启了一个进程),因此进程是动态的.系统运行一个程序即是一个程序从创建.运行到消亡的过程. 在 ...
- 浏览Github必备的5款神器级别的Chrome插件
我们知道 Github 是程序员特有的宝藏,也可以称它为 GayHub, 大家浏览 Github 的时候,一定遇到过下面这些问题: 不克隆到本地的情况下阅读代码困难. 无法单独下载仓库中的某个文件/文 ...
- 『无为则无心』Python基础 — 4、Python代码常用调试工具
目录 1.Python的交互模式 2.IDLE工具使用说明 3.Sublime3工具的安装与配置 (1)Sublime3的安装 (2)Sublime3的配置 4.使用Sublime编写并调试Pytho ...
- Python语言规范之Pylint的使用
1.Pylint是什么 pylint是一个Python源代码中查找bug的工具,能找出错误,和代码规范的运行.也就是你的代码有Error错误的时候能找出来错误,没有错误的时候,能根据Python代码规 ...
- 在element的table修改事件中修改数据,table的数据也会修改
大家在修改的时候有的会通过点击事件里面获取点击列表的值然后去赋值,但是row是Object对象类型,如果直接赋值的话,就变成了浅拷贝,复制的是地址,导致在表单中改变值的时候table中的数据也跟着改变 ...
