【论文考古】量化SGD QSGD: Communication-Efficient SGD via Gradient Quantization and Encoding

D. Alistarh, D. Grubic, J. Li, R. Tomioka, and M. Vojnovic, “QSGD: Communication-Efficient SGD via Gradient Quantization and Encoding,” Advances in Neural Information Processing Systems, vol. 30, 2017, Accessed: Jul. 31, 2021. [Online]. Available: https://proceedings.neurips.cc/paper/2017/hash/6c340f25839e6acdc73414517203f5f0-Abstract.html

作为量化SGD系列三部曲的第二篇，本篇文章是从单机学习到联邦学习的一个重要过渡，在前人的基础上重点进行了理论分析的完善，成为了量化领域绕不开的经典文献。

简介

相较于上一篇IBM的文章，本文考虑用梯度量化来改善并行SGD计算中的通信传输问题，并重点研究了通信带宽和收敛时间的关系（precision-variance trade-off）。具体而言，根据information-theoretic lower bounds，当调整每次迭代中传输的比特数时，梯度方差会发生改变，从而进行收敛性分析。实验结果表明在用ResNet-152训练ImageNet时能带来1.8倍的速率提升。

观点

• QSGD基于两个算法思想
  • 保留原始统计性质的随机量化（来源于量化SGD的实验性质）
  • 对量化后梯度的整数部分有损编码（进一步降低比特数）
• 减少通信开销往往会降低收敛速率，因此多训练带来的额外通信次数值不值，是神经网络量化传输需要考虑的重点
• 可以把量化看作一个零均值的噪声，只是它碰巧能够让传输更加有效
• 卷积层比其他层更容易遭受量化带来的性能下降，因此在量化方面，完成视觉任务的网络可能比深度循环网络获益更少

理论

• 方差对于SGD收敛性的影响

  

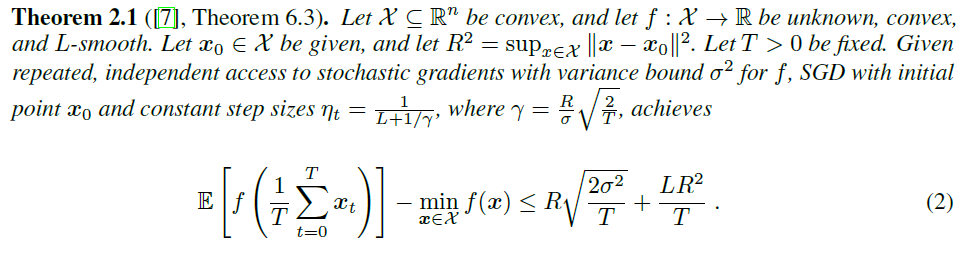
  mini-batch操作可以看作是减少方差的一个方法，当第一项主导的时候，由于方差减少到了\(\sigma^2 /m\)，因此收敛所需的迭代次数变为\(1/T\)

• 无损的parallel SGD就是一种mini batch，因此将定理换一种写法（其实就是写成不等式右边趋于零时），得到收敛所需迭代次数与方差的关系

  
  

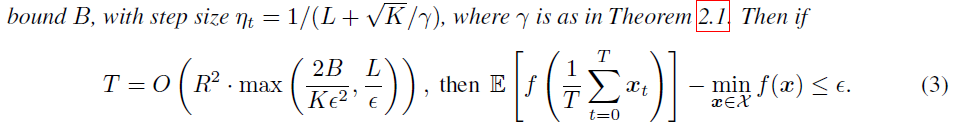
  通常第一项会主导迭代次数，因此结论：收敛所需的迭代次数与随机梯度的二阶方差界\(B\)成线性关系

• 随机量化与编码

  • 随机量化

    量化水平数量\(s\)（没有包含0），量化水平在\([0,1]\)均匀分布。构造的目的为：1）preserves the value in expectation；2）introduce minimal variance。

    

    • 对于向量中的每个分量单独量化
    • 进行\(|v_i|/\|v\|_2\)操作后能保证每个分量都落在\([0,1]\)区间内，从而转化为\([0,1]\)上的量化
    • 最终的上下取值概率之比就是量化点到上下量化水平的距离之比

    好像和投影距离是等价的？

    如此量化后有良好的统计特性（在这个量化值下有最小的方差）

    

  • 编码

    Elias integer encoding，基本思想是大的整数出现的频率会更低，因此循环的编码第一个非零元素的位置

    将整数转变为二进制序列，编码后的长度为\(|\operatorname{Elias}(k)|=\log k+\log \log k+\ldots+1 \leq(1+o(1)) \log k+1\)

  可得在给定量化方差界\(\left(\|v\|_{2}, \sigma, \zeta\right)\)后，需要传输的比特数上界为

  
  

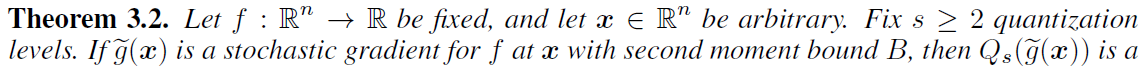
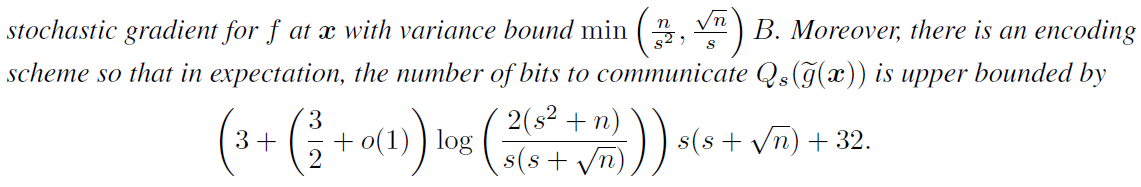
  注：此时1bit传输作为\(s=1\)的稀疏特例

• 将两个定理合并后的结果如下。由于QSGD计算的是接口变量方差，因此可以很便利地结合到各种与方差相关的随机梯度分析框架中。

  • Smooth convex QSGD

    

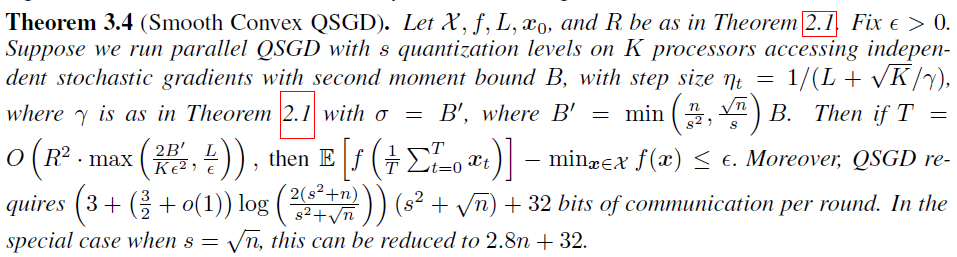
  • Smooth non-convex

    

• QSGD在实际应用中的两个变种

  • 将一个向量进一步分为若干bucket来量化，显然bucket size越大方差越大
  • 在向量scaling的时候选用最大分量值而不是向量的二范数

实验

• 全精度SGD传\(32n\)比特，QSGD最少可以只传\(2.8n+32\)比特，在两倍迭代次数下，可以带来节约\(5.7\)倍的带宽

• 实验结果

  • 性能上几乎超越了大模型

    

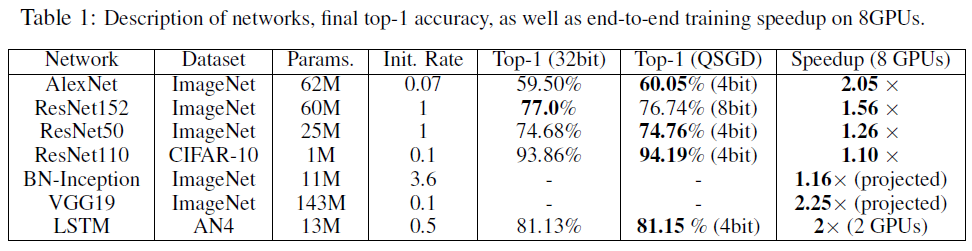
    • 要用大模型才有量化的价值

    We will not quantize small gradient matrices (< 10K elements), since the computational cost of quantizing them significantly exceeds the reduction in communication.

  • 计算和通信的开销

    

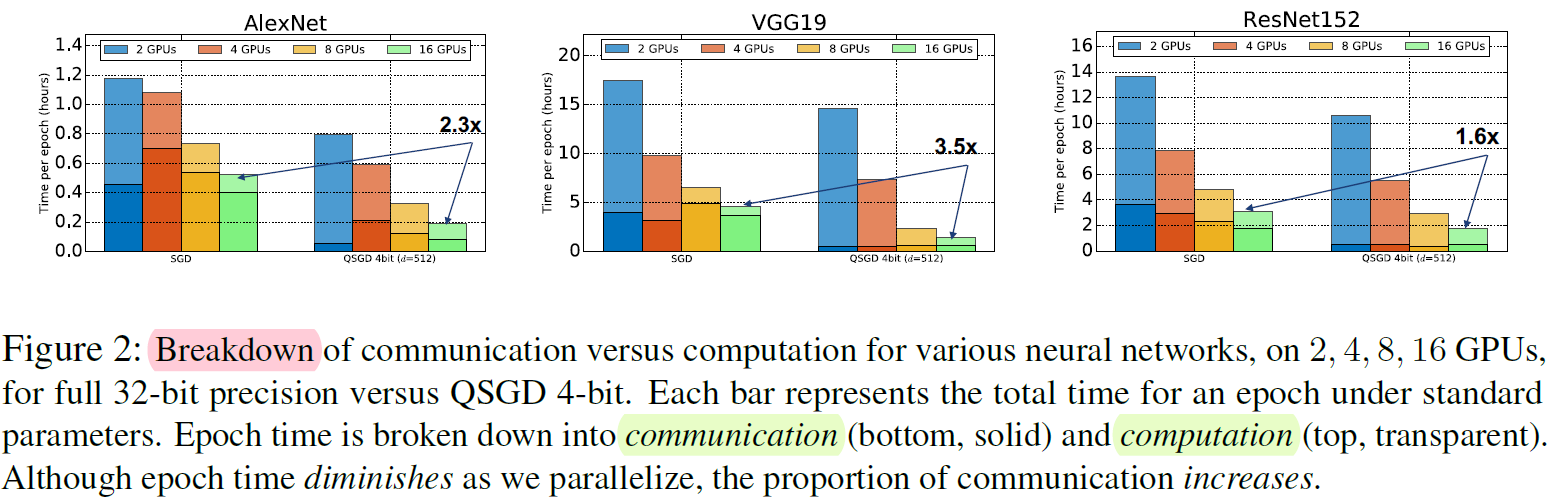
    • 增加并行后主要耗时在通信上

• 实验部分还没有完全搞懂（比如protocol部分、GPU的并行）

借鉴

• 文章在QSGD的基础上，从stochastic variance-reduced variant角度又继续分析QSVRG，覆盖到了指数收敛速率。也就是通过添加新技术来说明原始方法的扩展性。
• 这篇文章的基础是communication complexity lower bound of DME，因此建立传输比特数和方差的关系是直接拿过来的。而方差和收敛性的分析也是常用的，因此在承认DME的基础上很容易得到tight bound。
• 这篇文章的写作并不算优秀，但是内容十分solid和extensive，绝对是经典之作。