hdu 3530 "Subsequence" （单调队列）

传送门

题意：

　　给出一个序列，求最长的连续子序列，使得 m ≤ Max-Min ≤ k

我的理解：

　　定义数组 a[] 存储输入的 n 个数；

　　定义两个双端队列：

　　deque<int >qMax,qMin;

　　qMax : 维护前 i 个数的最大值（非递增序列）；

　　qMin : 维护前 i 个数的最小值（非递增序列）；

 for(int i=;i <= n;++i)
 {
     ///注意此处用了'=',也就是说，队列中的所有数都互异
     while(!qMax.empty() && a[qMax.back()] <= a[i])
         qMax.pop_back();///保证qMax递减
     qMax.push_back(i);
     while(!qMin.empty() && a[qMin.back()] >= a[i])
         qMin.pop_back();///保证qMin递增
     qMin.push_back(i);
 }

　　例如：

　　　　1　　2　　3　　4　　5　　6

　　val:  9　　6　　5　　1　　2　　3

　　i = 6 时的队列情况（此处队列中维护的是值，便于理解）:

　　　　qMax : {9,6,5,3};

　　　　qMin : {1,2,3};

　　假设来到 i 位置（队列维护下标）：

　　qMax : { φ₁,φ₂,φ₃,...,i };（下标递增，下标对应的值递减）

　　qMin : { ω₁,ω₂,ω₃,....,i }:（下标递增，下标对应的值递增）

　　

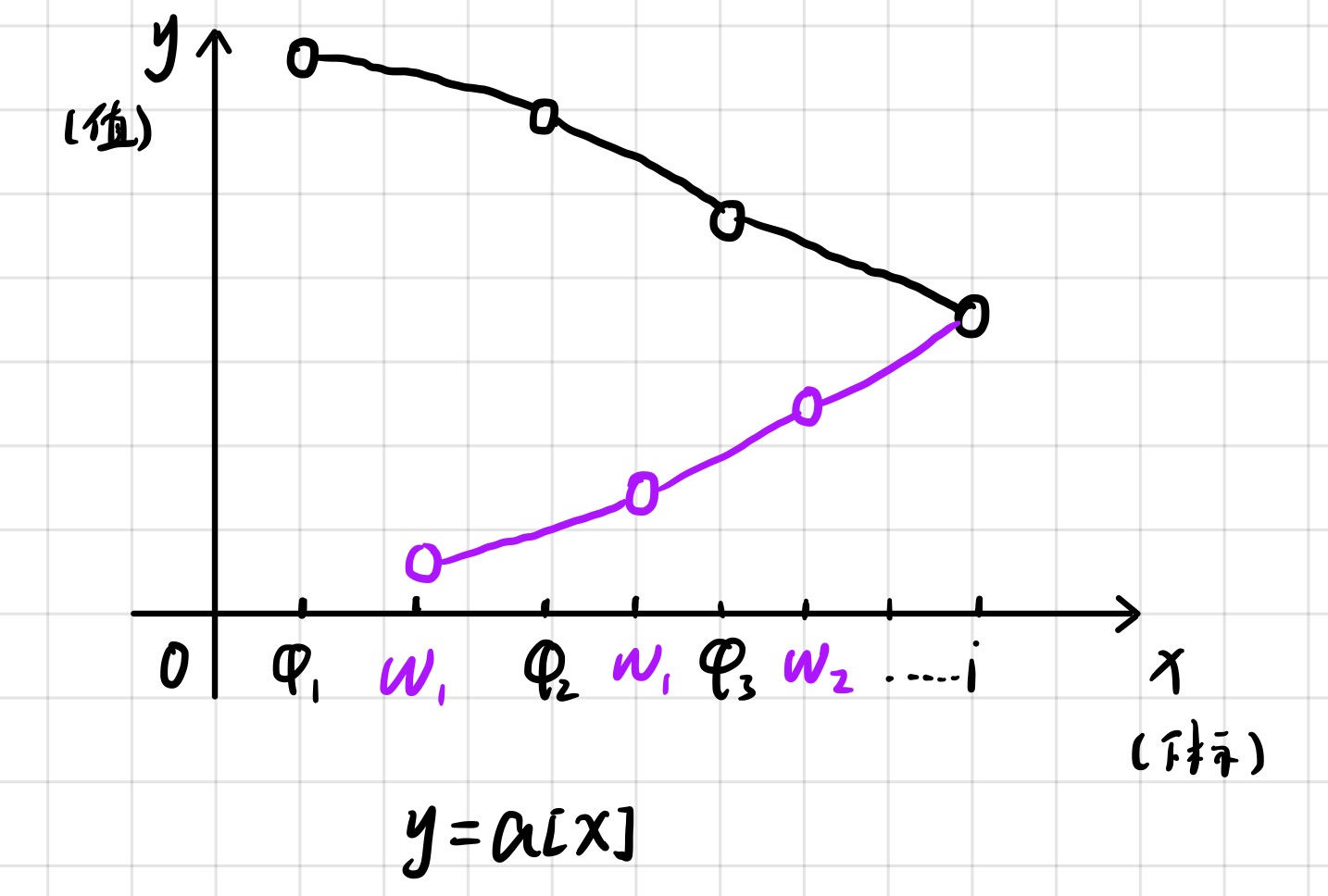
　　　　（φ₁,φ₂,φ₃,...ω₁,ω₂,ω₃ 互不相同，当然 i 除外）

　　　　（qMax.val ≥ qMin.val，下标对应的值）

　　下面看看队列的操作（pos初始为1)：

 while(a[qMax.front()]-a[qMin.front()] > k)
 {
     if(qMax.front() < qMin.front())
     {
         pos=qMax.front()+;
         qMax.pop_front();
     }
     else
     {
         pos=qMin.front()+;
         qMin.pop_front();
     }
 }
 if(a[qMax.front()]-a[qMin.front()] >= m)
     ans=max(ans,i-pos+);

　　首先判断 qMax.front() 对应的值（假设为 a[φ₁]） 与 qMin.front() 对应的值（假设为 a[ω₁]）做差是否大于 k；

　　如果大于，那么，如何使差值变小呢？

　　操作①qMax.pop_front()，（φ₁ -> φ₂）下一位对应的值更小

　　操作②qMin.pop_front()，（ω₁ -> ω₂）下一位对应的值更大

　　操作①②都可以使他们两者的差值变小，那么，到底该用哪个操作呢？

　　答案：谁的下标小，弹出谁，并且，所有的出队操作是不可能使队列为空的，因为两个队列中都有a[ i ]这个元素；

　　为什么要这么做呢？

　　假设不这么做，那么就是谁的下标大，弹出谁，假设 φ₁ > ω₁ ；

　　那么，就需要弹出φ₁ ，那么，包含当前最值的区间为[ ω₁ ,φ₂]，但是，φ₁ 也在其中，最大值就不该是a[φ₁ ]而应该是a[φ₂]；

　　所以，谁的下标小，弹出谁；

　　pos作用又是啥呢？

　　找到包含 a[ i ] 的，并且满足条件的最大的区间，也就是[pos,i]是包含a[i]的最大的区间；

　　那，为什么pos=front()+1就一定对呢？

　　假设当前弹出的是φ₁ ，也就是说a[φ₁]-a[ω₁] > t，假设 a[φ₂]-a[ω₁] ≤ t；

　　那么，a[pos]-a[ω₁] ≤ t；

　　因为a[pos] ≤ a[φ₂]，在 φ₂ 满足条件的情况下，pos一定满足条件，且是满足条件的最大的区间（φ₁不满足）；

　　为什么不用判断其是否 ≥ m 呢？

　　因为操作①②都是使差值减小，只有可能在后面的更新队列的操作中使其差值增大；

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<deque>
 using namespace std;
 const int maxn=1e5+;

 int n,m,k;
 int a[maxn];
 deque<int >qMax,qMin;

 int Solve()
 {
     qMax.clear();
     qMin.clear();

     int ans=;
     int pos=;
     for(int i=;i <= n;++i)
     {
         ///注意此处用了'=',也就是说，队列中的所有数都互异
         ///不加'='也行，不影响答案，因为在弹出操作时，qMax,qMin都将等于a[i]的给去了
         ///那么，a[i]本身是不会更新pos的值
         ///就算是队列末尾有重复的a[i]也不会更新pos，这就保证了pos的正确性
         ///[pos,i]是包含a[i]的最大的区间
         while(!qMax.empty() && a[qMax.back()] <= a[i])
             qMax.pop_back();
         qMax.push_back(i);
         while(!qMin.empty() && a[qMin.back()] >= a[i])
             qMin.pop_back();
         qMin.push_back(i);

         while(a[qMax.front()]-a[qMin.front()] > k)///最坏的情况是最后两个队列只剩下a[i]
         {
             if(qMax.front() < qMin.front())
             {
                 pos=qMax.front()+;
                 qMax.pop_front();
             }
             else
             {
                 pos=qMin.front()+;
                 qMin.pop_front();
             }
         }
         if(a[qMax.front()]-a[qMin.front()] >= m)
             ans=max(ans,i-pos+);///判断[pos,i]区间是否更新ans
     }
     return ans;
 }
 int main()
 {
     while(~scanf("%d%d%d",&n,&m,&k))
     {
         for(int i=;i <= n;++i)
             scanf("%d",a+i);
         printf("%d\n",Solve());
     }
     return ;
 }